CPhill

Y

        80

X            Z

tan Y  =  3/2  = XZ / XY    then  XZ =  (3/2)XY

So

(XY)^2  + [(3/2) XY]^2  = 80^2

XY^2  + (9/4)XY^2  = 6400

(13/4)XY^2  =  6400

XY^2  =   6400 ( 4 /13)

XY^2  =  (6400 * 4)  / 13

XY  = 80 * 2   / sqrt (13)

XY  =  160/ sqrt (13)  

144 * 12  = 1728 notes

1728 notes  / 560 (notes/min)   =  108/35  min

(108/35)min * 60 sec / 1 min   ≈   185 seconds

3m + 4n =  47     (1)

m + n =  15-2m   →  3m + n  =  15  →  n = 15 - 3m    (2)

Sub (2)  into (1)

3m + 4 (15 - 3m)  =  47

3m + 60 -  12m =  47

-9m =  47 - 60

-9m = -13

m = 13 /  9

At what value of x  is y = -1  ???

That x value =  c

Rearrange as

x^2 + 14x - 16  = 0

Sum of roots  =  a + b =  -14

Product of roots  = ab  =  -16

(2a - 3) ( 4b - 6)  =

12ab - 12a - 12b + 18 =

12ab -12 (a + b) + 18 =

12 (-16) - 12 (-14) + 18 =

-192 + 168 + 18  =

-6

Yep...I agree, nerdiest  !!!!

P of choosing the correct floor = ( 3/5 )

P of choosing the correct room on one of these floors = (3/10)

P ( choosing the correct floor and correct room )  =  (3/5) (3/10) =  9 / 50

f(y)  =   1/(y - 2)  + 1/(y - 8)

No denominator can =  0

So...the domain  is    (-inf , 2) u (2 , 8) U (8, inf )

See the image below :

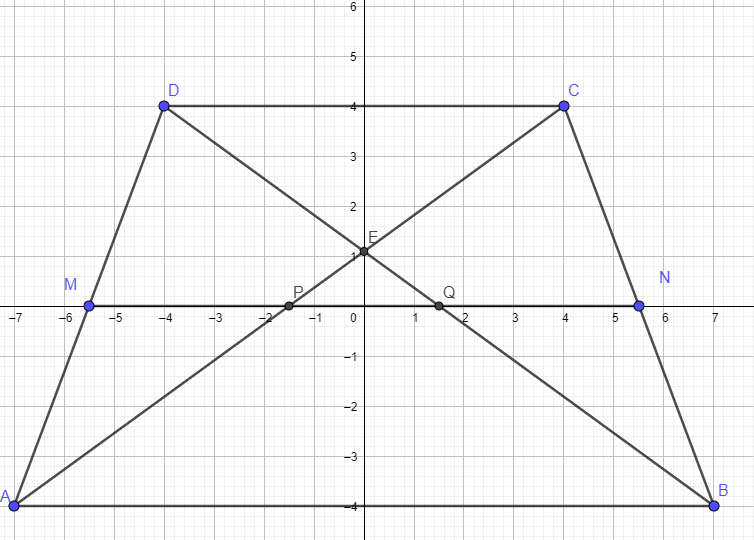
The length of the midsegment = (sum of bases ) / 2  =  (14 + 8)  / 2  =   11

For convenience, let the height of the trapezoid =  8    (it could be any height ....it works out the same)

Note that  DEC is similar to triangle BEA

Therefore  the height of triangle DEC =  (8/14)  =  of triangle BEA

So...the height of triangle  DEC  =  8 / (8 + 14) * (8)  =   (8/22)(8)  = 64/22 = 32/11

So  the height of triangle QEP =  4  - (32/11)  = 12/11 

And triangles DEC and QEP are similar

So  PQ =  (12/32)(8)  = 96/32  =  3

And, by symmetery , PQ = QN =  (11 - PQ) / 2  =   (11 - 3) / 2   =  8/2 =  4

x^2  + 3x  + c - 7x + x^2   =  -2

2x^2 - 4x + c  =  -2

[2x^2 - 4x + 2] + c  =  0

The  parabola  2x^2 - 4x + 2   has its vertex at  [ 4] / [ 2*2 ] =  1

And the y value here is  0

So  c =  0