CPhill

The repeated root comes from

8x^2  -32x + 32  = 0

8 ( x^2 - 4x + 4) = 0

x^2 - 4x + 4  = 0

(x - 2)^2  = 0

The repeated root  is   x  = 2

Sum of the roots = r + s  =    -4/3   square both sides

r^2 + 2rs + s^2  =  16/9

Product of the roots =  rs =  -12/3 = 4

2rs =  8

So

r^2 + 2rs + s^2 =  16/9

r^2 + 8  + s^2  =  16/9

r^2 + s^2 =   16/9   - 8

r^2 + s^2  = -56/9

This triangle is obtuse.. altitude CD falls outside triangle ABC  as shown

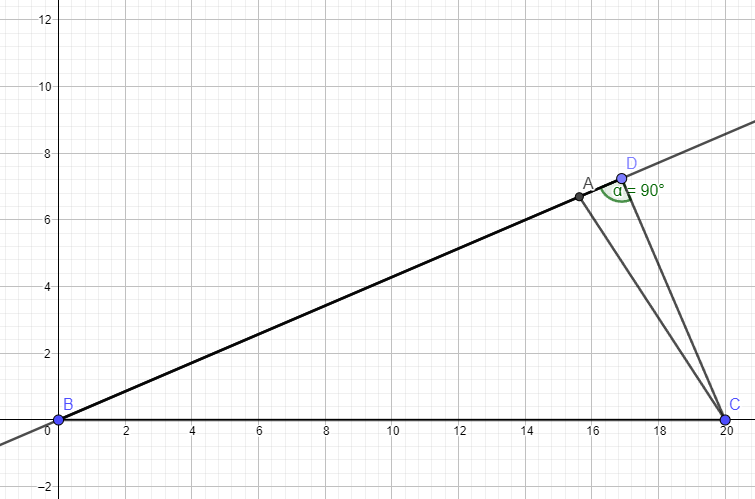
Let x be the distance from A to D

We have that

DC^2 = BC^2 +  (AB + x)^2 =   20^2  - (17+x)^2

DC^2 = (AC)^2  - x^2  =    8^2  - x^2

So

20^2 - (17+x)^2 = 8^2 - x^2

400 - x^2 - 34x -289  = 64 - x^2

-34x  =  289 + 64 - 400

-34x = -47

x = 47/34

DC =  sqrt [8^2 - (47/34)^2 ]

Area of ACD =   (1/2) (AD) (CD)  =      (1/2)(47/34)(sqrt [ 8^2 - (47/34)^2 ]   =   5.446 

Here's heureka's neat solution to  this :

https://web2.0calc.com/questions/pls-help_82

x sqrt (x)  =  x^(1 +1/2)  =  x^(3/2)

sqrt (x * sqrt (x))  =  sqrt (x^3/2) =  (x^3/2)^(1/2)   =  (x^3/4)

x * [sqrt (x *sqrt (x) ]   =  x*  x^(3/4) =  x ^(1 + 3/4)  = x^(7/4)

sqrt [ x *  [sqrt (x *sqrt (x)] ] =   (x^7/4)^(1/2 ) =    x^(7/8)

Any 

2^(2n - 1)   will not be an integer power of 4

When n =  1,     2^(2n-1) =   2^1  =   2

When n = 10,  2^(2*10  - 1) =  2^19  = 524,888

So

10  are integer powers of 2 but not powers of 4

Since the sine of   a reference angle in the  1st quadrant = the sine of the  same  reference angle in the  second quadrant....we have that.....

(180   - 5theta) =  theta

180  =  6 theta

180 / 6  =  theta =   30°

tan  (2 theta)  =  tan (60°) =     sqrt (3)

We only need to  calculate these

19  -17 =   2

19 - 15 =   4

19 -  13  = 6

19 - 11   = 8

19 - 9  = 10

19 - 7 =  12

19  - 5 =   14

19 - 3 = 16

19 -1  = 18

So....9 distinct (different) positive differences are possible

Volume = pi (h/3)(a^2 + ab + b^2)     where h is the  height and  a, b are the radii 

Surface area  = pi  [ (a + b) sqrt   [ ( a  -b)^2 + h^2 ]  + a^2 + b^2  ] 

Filling in what we know

pi [ (9 +12) sqrt [ (12 - 9 )^2 + 4^2 ] + 12^2 + 9^2  ]  = 330pi  = A

pi (4/3) (12^2 + 12*9 + 9^2  ]  =  444pi  =  V

A + V =     330pi + 444 pi  =   774 pi   

Multiply the first equation  through by 2

s + 10t = 6    →   s  =  6 - 10t

Sub this into the second equation

3t  - 6(6 - 10t)  = 9 + 5t

3t  - 36 + 60t  = 9 + 5t

63t - 36  = 9 + 5t

63t  -5t  = 9 + 36

58t  =  45

t =  45 /  58

s = 6 - 10( 45 /58)   =    -51/29