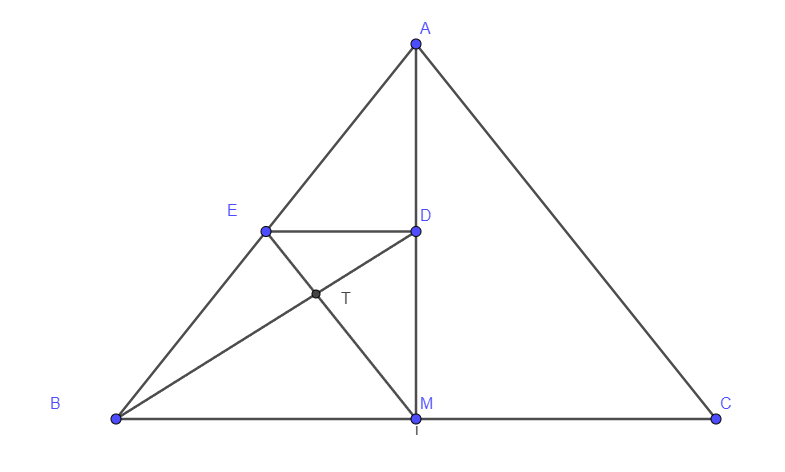
Area of ABC = (1/2)AM (BC)
20 = (1/2) AM * BC
40 = AM *BC
Triangle BAM similar to Triangle EAD
Since ED is the midpoint of AB, then ED = (1/2) BM
And ED parallel to BM....so.....Triangle ETD is similar to Triangle MTB
And since DE = (1/2)BM , then the height of trapezoid EDMB has three equal parts and the height of MBT = 2 of them....so height of MBT = (2/3) (1/2)AM = (1/3(AM)
And BM = (1/2)BC
So....the area of MBT = (1/2)(1/3)AM * BM = (1/2)(1/3)AM *(1/2)BC = (1/12) AM * BC
And triangle EBM has a height of (1/2)AM and base = BM
So....its area = (1/2) BM * (1/2)AM = (1/2) (1/2)BC * (1/2)AM = (1/8) AM * BC
So [ BET ] = [EBM ] - [ MBT ] = (1/8 - 1/12) AM *BC = (1/24)AM *BC = (1/24) (40) = 5 / 3


