CPhill

Factor  2700  =  2^2 * 3^3 * 5^2  =  2*2*3*3*3*5*5

Possible Rolls                  Identifiable Sequences

22333551                         8! / ( 2! * 3! * 2!)  =   1680

43335511                         8!  /  (3! * 2! * 2!)  =  1680 

62335511                         8!  / (2! * 2! * 2!)   =  5040

66355111                         8!  /  (2! * 2! * 3!)  =  1680       

Identifiable sequences  =  3(1680) + 5040 =  10080

(0, 0)        (1,  1)

(2, 0)        (1, -1)

(-2,0)        (-1, 1)

(0,-2)        ( -1,-1)

(0, 2)

3331  =    4! / 3! =  4 integers

5311  =    4! / 2! =  12 integers

16 integers

                                             A

                            E                      D

                                  T

                B                         M                  C

Height of ABC  =  AM

Base of ABC = BC

[ ABC ]  = (1/2) (BC) (AM) =  14   → (BC) (AM)  =  28

Height of BEC   = (1/2)AM

Base of BEC =  BC

[ BEC ]  = (1/2) (BC) (1/2)AM =  (1/4)(BC) (AM)  =  (1/4) (28)  =  7

A

4                5

B           D            C

              3

Since AD bisects  angle BAC

Then  let DC=  x  and BD = 3 -x

So

(3 - x) / 4 = x / 5

5 (3 -x)  = 4x

15 - 5x = 4x

15 = 9x

x = 15/9  = 5/3

Height of triangle ADC = 4   base = (5/3)

Area =  (1/2) (5/3) 4  =  20 /  6  =  10/3  =  3  (to the nearest integer )

This  boils down to  finding the circumradius of the  circle

We have an inscribed triangle ABC

Semi-perimeter  =  [ 8 + 15 + 12 ]   / 2   =   17.5

Area =  sqrt [ (17.5 ) (17.5 - 8) (17.5 - 15) (17.5 - 12) ]  =  sqrt [ 2285.9375 ] 

Circumradius =   product of the  sides /  4 * Area  =

(8 * 15 * 12)  /(4 sqrt [ 2285.9375] ≈  7.53  =  radius of the  circle

N33E  =  57°

N84E =   6°

S70E  = 340°

4cos 57°  + 5cos 6° + 4.5cos 340°  ≈  11.38

4sin 57° + 5sin 6° + 4.5sin 340°  ≈ 2.34

Direction  =   arctan ( 2.34 / 11.38) ≈ 11.6°  =  N 78.4 E

Magnitude  = sqrt [ 11.38^2 + 2.34^2 ]  ≈  11.61  N

A circle is centered at  The tangent to the circle at  is extended to  Line segment  intersects the circle at  Find the area of the circle.      Measures = OS = 3,   SR = 4,   RQ = 4,  PQ = 8

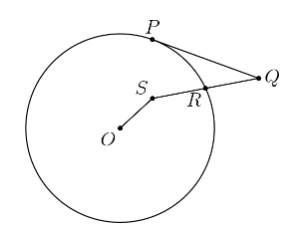
Draw QS in the direction of S through to M where M  is  on the circle

Secant-Tangent Theorem

PQ^2  = RQ( RQ +RM)

8^2  =  4 ( 4 + RM)

64 / 4  = 4 + RM

16 = 4 + RM

RM = 16 - 4

RM = 12

SM  = RM - SR  = 12 - 4 = 8

Connect OR, OM  =   radius of the circle = r

Note that cos RSO   =  - cos MSO

By the Law of Cosines

r^2  = SR^2 + SO^2 - 2(SR * SO) (-cos MSO)

r^2  = SM^2 + SO^2 - 2(SM * SO) cos (MSO)     simplify this  system

r^2  = 4^2 + 3^2  +2 ( 4 * 3) cos (MSO)     (1)

r^2  = 8^2 + 3^2 - 2(8*3) cos (MSO)

4^2 + 3^2 + 24 cos (MSO)  = 8^2 + 3^2 - 48cos (MSO)

25 + 24cos (MSO) = 73 - 48 cos (MSO)

72 cos MSO = 48 

cos MSO = 48/72  =  2/3      (2)

Sub (2)  into (1)

r^2  = 4^2 + 3^2 + 2 (4 *3)(2/3)

r^2 = 25 + 16

r^2 = 41

Area of circle =  pi * r^2  =  41 pi

Here : https://web2.0calc.com/questions/geometry_55509

Here :  https://web2.0calc.com/questions/polygon_74