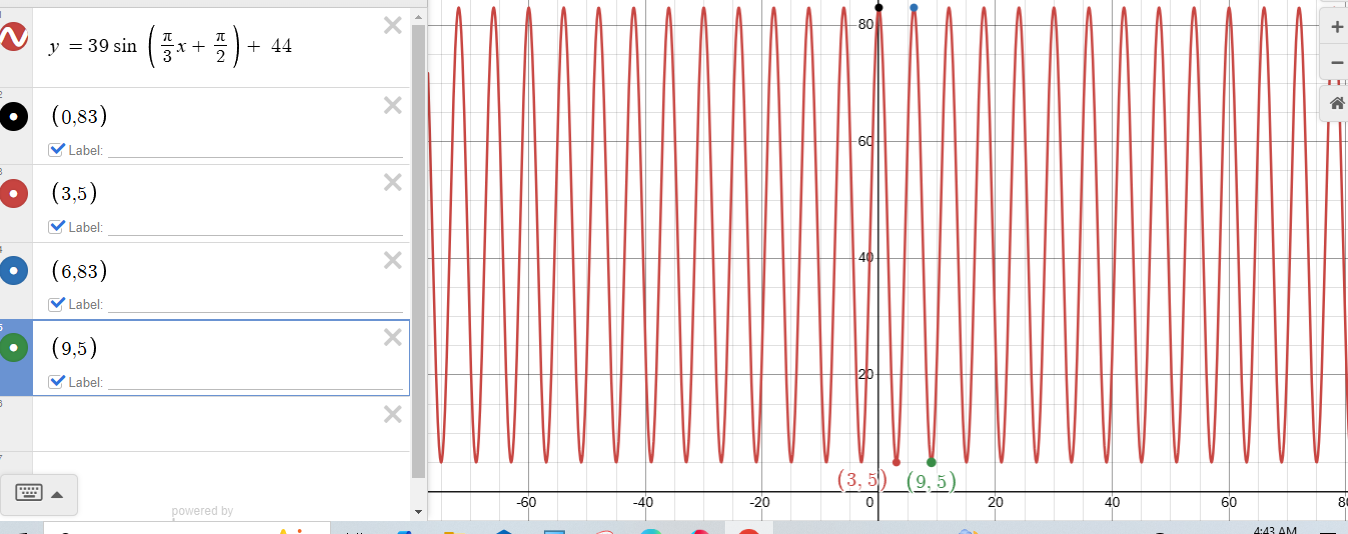
3. At a dock on the east coast, low tide occurs at 3 p.m. with a water depth of 5ft. The depth at high tide is 83 ft. High tide occurs every 6 hours. Explain how to find the sinusoidal function that models the depth in terms of time, X.
The function will be
y = A cos (Bx + C) + D
High tide will occur at noon and 6 PM
Low tide occurs at 3PM and 9PM
The period = 6
So
2pi / B = 6
B = (2/6)pi = pi/3
Amplitude = A = (high point -low point)/ 2 = (83 - 5) / 2 = 39
D = (high point + low point) / 2 = (83 + 5) / 2 = 44
Let noon be x = 0
The hardest thing to figure is "C"
When x= 0, y= 83 we can solve for "C" thusly
y = 39sin (pi/3 *x + C) + D
83 = 39 sin (pi/3 * 0 + C) + 44
39 = 39 sin (C)
39/39 = sin (C)
1 = sin (C)
arcsin (1) = C
We are asking....where is the sin = 1 ??? answer...at pi/2
arcsin (1) = pi/2 = C
So...our function is
y = 39 sin (pi/3 * x + pi/2) + 44
Here's the graph