homework questions
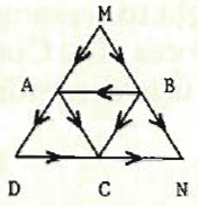
Using only the paths and directions shown, how many different routes are there from M to N?
Adjacency matrix directed: Source: https://en.wikipedia.org/wiki/Adjacency_matrix
If A is the adjacency matrix of the directed or undirected graph G,
then the matrix A^n (i.e., the matrix product of n copies of A) has an interesting interpretation:
the element (i, j) gives the number of (directed or undirected) walks of length n from vertex i to vertex j.
\(A = \begin{array}{|c|c|c|c|c|c|c|} \hline & M & A & B & D & C & N \\ \hline M & 0 & 1 & 1 & 0 & 0& \color{red}0 \\ \hline A & 0 & 0 & 0 & 1 & 1& 0 \\ \hline B & 0 & 1 & 0 & 0 & 1& 1 \\ \hline D & 0 & 0 & 0 & 0 & 1& 0 \\ \hline C & 0 & 0 & 0 & 0 & 0& 1 \\ \hline N & 0 & 0 & 0 & 0 & 0& 0 \\ \hline \end{array} ~\text{There is $0\times$ 1-way route }\)
\(A^2 = \begin{array}{|c|c|c|c|c|c|c|} \hline & M & A & B & D & C & N \\ \hline M & 0 & 1 & 0 & 1 & 2 & \color{red}1 \\ \hline A & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \hline B & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \hline D & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \hline C & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \hline N & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \hline \end{array} ~\text{There is $1\times$ 2-way route }\)
\(A^3 = \begin{array}{|c|c|c|c|c|c|c|} \hline & M & A & B & D & C & N \\ \hline M & 0 & 0 & 0 & 1 & 2 & \color{red}2 \\ \hline A & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \hline B & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \hline D & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \hline C & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \hline N & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \hline \end{array} ~\text{There are $2\times$ 3-way routes }\)
\(A^4 = \begin{array}{|c|c|c|c|c|c|c|} \hline & M & A & B & D & C & N \\ \hline M & 0 & 0 & 0 & 0 & 1 & \color{red}2 \\ \hline A & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \hline B & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \hline D & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \hline C & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \hline N & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \hline \end{array} ~\text{There are $2\times$ 4-way routes }\)
\(A^5 = \begin{array}{|c|c|c|c|c|c|c|} \hline & M & A & B & D & C & N \\ \hline M & 0 & 0 & 0 & 0 & 0 & \color{red}1 \\ \hline A & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \hline B & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \hline D & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \hline C & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \hline N & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \hline \end{array} ~\text{There is $1\times$ 5-way route }\)
\(A^6 = \begin{array}{|c|c|c|c|c|c|c|} \hline & M & A & B & D & C & N \\ \hline M & 0 & 0 & 0 & 0 & 0 & \color{red}0 \\ \hline A & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \hline B & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \hline D & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \hline C & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \hline N & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \hline \end{array} ~\text{There is $0\times$ 6-way routes }\)
1+2+2+1 = 6 different routes are there from M to N
![]()