heureka

Four points \(A_1,\ A_2,\ A_3,\ \)and \(A_4\) are chosen at random on a circle.
Find the probability that chords \(\overline{A_1 A_2}\) and \(\overline{A_3 A_4}\) intersect.

My attempt:

\(\begin{array}{|r|cl|} \hline & & \text{intersect} \\ \hline & 2~3 \\ 1 & 1~~~4 \\ \hline & 2~4 \\ 2 & 1~~~3 \\ \hline & 3~2 \\ 3 & 1~~~4& \checkmark\\ \hline & 3~4 \\ 4 & 1~~~2 \\ \hline & 4~2 \\ 5 & 1~~~3 & \checkmark\\ \hline & 4~3 \\ 6 & 1~~~2 \\ \hline & 1~3 \\ 7 & 2~~~4 \\ \hline & 1~4 \\ 8 & 2~~~3 \\ \hline & 3~1 \\ 9 & 2~~~4 & \checkmark\\ \hline & 3~4 \\ 10 & 2~~~1 \\ \hline & 4~1 \\ 11 & 2~~~3& \checkmark\\ \hline & 4~3 \\ 12 & 2~~~1 \\ \hline & 1~2 \\ 13 & 3~~~4 \\ \hline & 1~4 \\ 14 & 3~~~2 & \checkmark\\ \hline & 2~1 \\ 15 & 3~~~4 \\ \hline & 2~4 \\ 16 & 3~~~1 & \checkmark\\ \hline & 4~1 \\ 17 & 3~~~2 \\ \hline & 4~2 \\ 18 & 3~~~1 \\ \hline & 1~2 \\ 19 & 4~~~3 \\ \hline & 1~3 \\ 20 & 4~~~2 & \checkmark\\ \hline & 2~1 \\ 21 & 4~~~3 \\ \hline & 2~3 \\ 22 & 4~~~1 & \checkmark\\ \hline & 3~1 \\ 23 & 4~~~2 \\ \hline & 3~2 \\ 24 & 4~~~1 \\ \hline \end{array}\)

The probability is \(\dfrac{8}{24} = \mathbf{\dfrac{1}{3}}\)

​geometry proof

\(\begin{array}{|rcll|} \hline \mathbf{\text{In ACP sin-rule:}} \\ \hline \frac{w}{\sin(90^\circ-\alpha)} &=& \frac{CP}{\sin(45^\circ)} \quad (1) \\ \hline \end{array} \begin{array}{|rcll|} \hline \mathbf{\text{In CPQ sin-rule:}} \\ \hline \frac{\sin(45^\circ)}{v} &=& \frac{\sin(\alpha)}{CP} \quad (2) \\ \hline \end{array} \\ \begin{array}{|lrcll|} \hline (1)\times(2): & \frac{w}{\sin(90^\circ-\alpha)}\times \frac{\sin(45^\circ)}{v} &=&\frac{CP}{\sin(45^\circ)} \times \frac{\sin(\alpha)}{CP} \\\\ & \frac{w}{\cos(\alpha)}\times \frac{\sin(45^\circ)}{v} &=&\frac{\sin(\alpha)}{\sin(45^\circ)} \\\\ & \frac{w}{v} &=& \frac{\sin(\alpha)\sin(\alpha)} {\sin^2(45^\circ)} \\\\ & \frac{w}{v} &=& \frac{2\sin(\alpha)\sin(\alpha)} {2\sin^2(45^\circ)} \\ & && \boxed{\sin(45^\circ) = \frac{\sqrt{2}}{2} \\ \sin^2(45^\circ) = \frac{1}{2} }\\ & \frac{w}{v} &=& \frac{2\sin(\alpha)\sin(\alpha)} {2*\frac{1}{2}} \\ & \frac{w}{v} &=& 2\sin(\alpha)\sin(\alpha) \\ & && \boxed{ 2\sin(\alpha)\sin(\alpha)= \sin(2\alpha) }\\ & \mathbf{\frac{w}{v}} &=& \mathbf{\sin(2\alpha)} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{\text{In BCQ sin-rule:}} \\ \hline \frac{u}{\sin(\alpha-45^\circ)} &=& \frac{CQ}{\sin(45^\circ)} \quad (3) \\ \hline \end{array} \begin{array}{|rcll|} \hline \mathbf{\text{In CPQ sin-rule:}} \\ \hline \frac{\sin(45^\circ)}{v} &=& \frac{\sin(135^\circ-\alpha)}{CQ} \quad (4) \\ \hline \end{array} \\ \begin{array}{|lrcll|} \hline (3)\times(4): & \frac{u}{\sin(\alpha-45^\circ)}\times \frac{\sin(45^\circ)}{v} &=&\frac{CQ}{\sin(45^\circ)} \times \frac{\sin(135^\circ-\alpha)}{CQ} \\\\ & \frac{u}{\sin(\alpha-45^\circ)}\times \frac{\sin(45^\circ)}{v} &=&\frac{\sin(135^\circ-\alpha)}{\sin(45^\circ)} \\\\ & \frac{u}{v} &=& \frac{\sin(\alpha-45^\circ)\sin(135^\circ-\alpha)} {\sin^2(45^\circ)} \\ & && \boxed{\sin(45^\circ) = \frac{\sqrt{2}}{2} \\ \sin^2(45^\circ) = \frac{1}{2} }\\ & \frac{u}{v} &=& \frac{\sin(\alpha-45^\circ)\sin(135^\circ-\alpha)} {\frac{1}{2}} \\\\ & \frac{u}{v} &=& 2\sin(\alpha-45^\circ)\sin(135^\circ-\alpha) \\ & && \boxed{\sin(135^\circ-\alpha) = \sin \Big(180^\circ-(135^\circ-\alpha) \Big)\\ = \sin(\alpha+45^\circ) }\\ & \frac{u}{v} &=& 2\sin(\alpha-45^\circ)\sin(\alpha+45^\circ) \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline && \mathbf{ \sin(\alpha-45^\circ)\sin(\alpha+45^\circ) } \\ &=&\Big(\sin(\alpha)\cos(45^\circ)-\cos(\alpha)\sin(45^\circ)\Big) \Big(\sin(\alpha)\cos(45^\circ)+\cos(\alpha)\sin(45^\circ)\Big) \\ && \boxed{ \cos(45^\circ)=\sin(45^\circ)=\frac{\sqrt{2}}{2} } \\ &=&\frac{\sqrt{2}}{2}\Big(\sin(\alpha)-\cos(\alpha)\Big) \frac{\sqrt{2}}{2}\Big(\sin(\alpha)+\cos(\alpha)\Big) \\ &=&\frac{1}{2}\Big(\sin(\alpha)-\cos(\alpha)\Big)\Big(\sin(\alpha)+\cos(\alpha)\Big) \\ &=&\frac{1}{2}\Big(\sin^2(\alpha)-\cos^2(\alpha)\Big) \\ &=&-\frac{1}{2}\Big(\cos^2(\alpha)-\sin^2(\alpha)\Big) \\ && \boxed{ \cos^2(\alpha)-\sin^2(\alpha)= \cos(2\alpha)} \\ &=&\mathbf{-\frac{1}{2}\cos(2\alpha)} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \frac{u}{v} &=& 2\sin(\alpha-45^\circ)\sin(\alpha+45^\circ) \\ \frac{u}{v} &=& 2\left(-\frac{1}{2}\cos(2\alpha)\right) \\ \mathbf{\frac{u}{v}} &=& \mathbf{-\cos(2\alpha)} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{\frac{w}{v}} = \mathbf{\sin(2\alpha)} &\qquad & \mathbf{\frac{u}{v}} = \mathbf{-\cos(2\alpha)} \\\\ \left( \frac{w}{v} \right)^2 + \left( \frac{u}{v} \right)^2 &=& \Big( \sin(2\alpha)\Big)^2 + \Big(-\cos(2\alpha)\Big)^2 \\ \left( \frac{w}{v} \right)^2 + \left( \frac{u}{v} \right)^2 &=& \sin^2(2\alpha) + \cos^2(2\alpha) \\ \frac{w^2}{v^2} + \frac{u^2}{v^2} &=& 1 \quad | \quad \times v^2 \\ \mathbf{w^2 + u^2} &=& \mathbf{v^2} \\ \hline \end{array}\)

Thank you, CPhill !

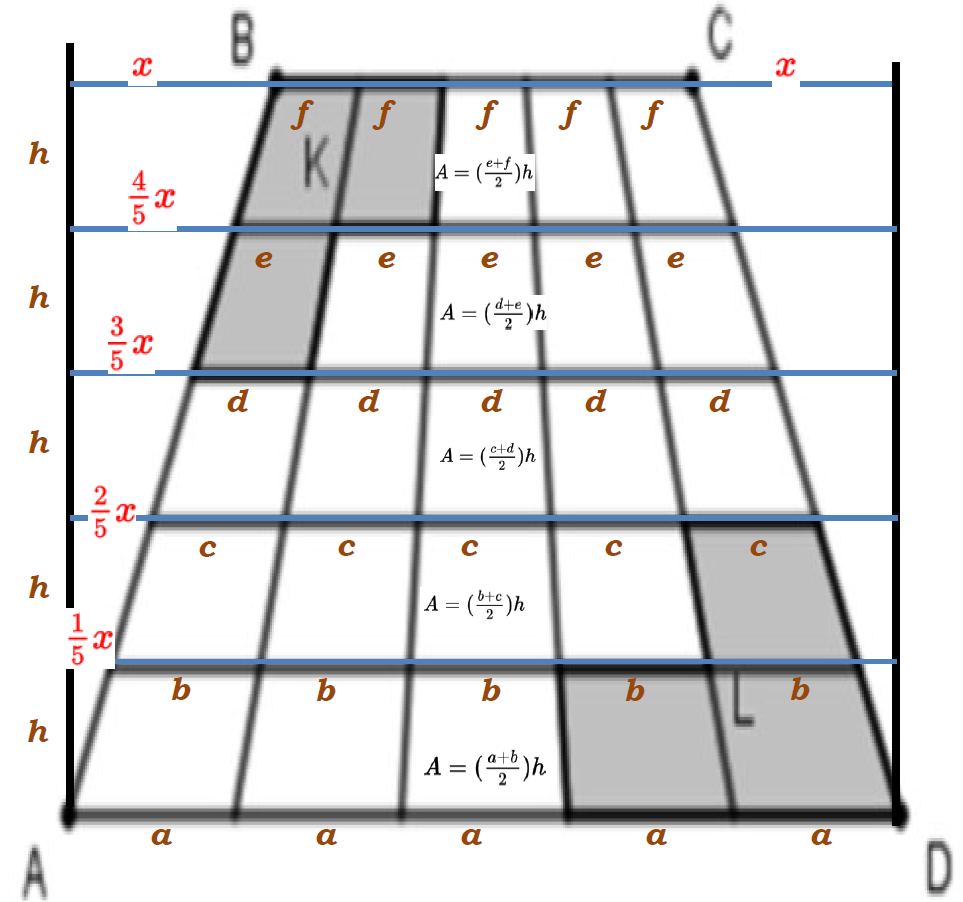
The trapezoid is divided into 5 parts horizontally with AB and CD are equally divided.
The Trapezoid also divided into 5 parts vertically with AD and BC are devided equally.
If the shaded regions K has area 35 and the shaded region L has area 55.
Determine the area of the trapezoid ABCD.

\(\begin{array}{|rcll|} \hline 5b+2*\frac{1}{5}x = 5a &\text{ or }& \boxed{b = a-\frac{2}{25}x} \\ 5c+2*\frac{2}{5}x = 5a &\text{ or }& \boxed{c = a-\frac{4}{25}x} \\ 5d+2*\frac{3}{5}x = 5a &\text{ or }& \boxed{d = a-\frac{6}{25}x} \\ 5e+2*\frac{4}{5}x = 5a &\text{ or }& \boxed{e = a-\frac{8}{25}x} \\ 5f+2x = 5a &\text{ or }& \boxed{f = a-\frac{2}{5}x} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \text{trapezoid } ABCD &=& \left(\dfrac{5a+5f}{2}\right)5h \quad | \quad \boxed{f = a-\frac{2}{5}x} \\ &=& \left(\dfrac{5a+5(a-\frac{2}{5}x)}{2}\right)5h \\ &=& \left(\dfrac{10a-2x}{2}\right)5h \\ &=& (5a-x)5h \\ \mathbf{\text{trapezoid } ABCD} &=& \mathbf{25ah-5xh} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{K:} \\ \hline 35 &=& \left(\frac{d+e}{2}\right)h + 2 \left( \frac{e+f}{2}\right)h \\ 35 &=& \left(\frac{d+e}{2}\right)h + ( e+f )h \\ 35 &=& \left(\frac{a-\frac{6}{25}x+a-\frac{8}{25}x}{2}\right)h + ( a-\frac{8}{25}x+a-\frac{2}{5}x )h \\ \ldots \\ \mathbf{35} &=& \mathbf{3ah-xh} \quad (1) \\ \hline \end{array} \)

\(\begin{array}{|rcll|} \hline \mathbf{L:} \\ \hline 55 &=& 2 \left( \frac{a+b}{2}\right)h + \left(\frac{b+c}{2}\right)h \\ 55 &=& ( a+b )h + \left(\frac{b+c}{2}\right)h \\ 55 &=& ( a+a-\frac{2}{25}x )h + \left( \frac{ a-\frac{2}{25}x + a-\frac{4}{25}x }{2} \right)h \\ \ldots \\ \mathbf{55} &=& \mathbf{3ah-\frac{5}{25}xh} \quad (2) \\ \hline \end{array} \)

\(\begin{array}{|lrcll|} \hline (2)-(1): & 3ah-\frac{5}{25}xh -(3ah-xh) &=& 55-35 \\ & 3ah-\frac{5}{25}xh -3ah+ xh &=& 20 \\ & -\frac{5}{25}xh + xh &=& 20 \\ & \frac{20}{25}xh &=& 20 \\ & \frac{xh}{25} &=& 1 \\ & \mathbf{xh} &=& \mathbf{25} \\\\ (1): & 3ah &=& 35+xh \\ & 3ah &=& 35+25 \\ & 3ah &=& 60 \\ & \mathbf{ah} &=& \mathbf{20} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{\text{trapezoid } ABCD} &=& \mathbf{25ah-5xh} \\ &=& 25*20-5*25 \\ &=& 500-125 \\ \mathbf{\text{trapezoid } ABCD} &=& \mathbf{375} \\ \hline \end{array} \)

Thank you, EpicWater !

Thank you, Alan !

Solve for x.

\(\begin{array}{|rcll|} \hline \mathbf{\text{cos-rule:}} \\ \hline \mathbf{z^2} &=& \mathbf{10^2+12^2-2*10*12*\cos(60^\circ)} \quad | \quad \cos(60^\circ) = \dfrac{1}{2} \\ z^2 &=& 100+144-240*\dfrac{1}{2} \\\\ z^2 &=& 124 \\\\ z^2 &=& 4*31 \\\\ \mathbf{z} &=& \mathbf{2\sqrt{31}} \qquad (1) \\ \hline \end{array} \)

\(\begin{array}{|rcll|} \hline \mathbf{\text{sin-rule:}} \\ \hline \mathbf{\dfrac{\sin(\alpha)}{10}} &=& \mathbf{\dfrac{\sin(60^\circ)}{z}} \\\\ \sin(\alpha) &=& \dfrac{10\sin(60^\circ)}{z} \quad | \quad \sin(60^\circ) = \dfrac{\sqrt{3}}{2} \\\\ \sin(\alpha) &=& \dfrac{10\sqrt{3}}{2z} \\\\ \sin(\alpha) &=& \dfrac{5\sqrt{3}}{z} \quad | \quad z=2\sqrt{31} \\\\ \sin(\alpha) &=& \dfrac{5\sqrt{3}}{2\sqrt{31}} \\\\ \sin(\alpha) &=& \dfrac{5}{62}\sqrt{93} \\\\ \sin(\alpha) &=& 0.77771377105 \\\\ \alpha &=& \arcsin\left(0.77771377105\right) \\\\ \mathbf{\alpha} &=& \mathbf{51.0517244354^\circ} \\ \hline \end{array} \)

\(\begin{array}{|rcll|} \hline \mathbf{\text{sin-rule:}} \\ \hline \mathbf{\dfrac{\sin(\alpha)}{10}} &=& \mathbf{ \dfrac{\sin(\beta)}{12}} \\\\ \sin(\beta) &=& \dfrac{12}{10}\sin(\alpha) \\\\ \sin(\beta) &=& \dfrac{6}{5}\sin(\alpha) \\\\ \sin(\beta) &=& \dfrac{6}{5}*0.77771377105 \\\\ \sin(\beta) &=& 0.93325652526 \\\\ \beta &=& \arcsin\left(0.93325652526\right) \\\\ \mathbf{\beta} &=& \mathbf{68.9482755646^\circ} \\ \hline \end{array} \)

\(\begin{array}{|rcll|} \hline \mathbf{\text{sin-rule:}} \\ \hline \mathbf{\dfrac{\sin(30^\circ+\alpha)}{x}} &=& \mathbf{ \dfrac{\sin(\beta)}{12}} \\\\ x &=& \dfrac{12\sin(30^\circ+\alpha)^\circ)}{\sin(\beta)} \\\\ x &=& \dfrac{12\sin(30^\circ+51.0517244354^\circ)}{0.93325652526} \\\\ x &=& \dfrac{12\sin(81.0517244354)}{0.93325652526} \\\\ x &=& \dfrac{12*0.98782916115}{0.93325652526} \\\\ x &=& \dfrac{11.8539499338}{0.93325652526} \\\\ \mathbf{x} &=& \mathbf{12.7017059222} \\ \hline \end{array} \)

Thank you, CPhill !

In triangle \(ABC\),  let \(I\) be the intersection of angle bisectors \(\overline{AD}\) and  \(\overline{BE}\).
Prove that \( \angle DIB = 90^\circ - \dfrac{\angle BCA}{2}\).  

\(\begin{array}{rcll} \begin{array}{|rcll|} \hline \mathbf{\text{In AIB:}} \\ \hline 180^\circ-x + \alpha + \beta &=& 180^\circ \\ -x + \alpha + \beta &=& 0 \\ \mathbf{x} &=& \mathbf{\alpha + \beta} \qquad (1) \\ \hline \end{array} & \begin{array}{|rcll|} \hline \mathbf{\text{In BID:}} \\ \hline x + D + \beta &=& 180^\circ \\ \mathbf{180^\circ-D} &=& \mathbf{x+\beta} \qquad (2) \\ \hline \end{array} \\ & \begin{array}{|rcll|} \hline \mathbf{\text{In EIA:}} \\ \hline x + E + \alpha &=& 180^\circ \\ \mathbf{180^\circ-E} &=& \mathbf{x+\alpha} \qquad (3) \\ \hline \end{array} \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{\text{In EIDC:}} \\ \hline (180^\circ-D)+(180^\circ-E)+(180^\circ-x) + C &=& 360^\circ\\ \boxed{ \mathbf{180^\circ-D=x+\beta}\\ \mathbf{180^\circ-E=x+\alpha}} \\ x+\beta+x+\alpha+(180^\circ-x) + C &=& 360^\circ \\ x+\beta+x+\alpha+180^\circ-x + C &=& 360^\circ \quad | \quad - 180^\circ \\ x+\beta+x+\alpha -x + C &=& 360^\circ - 180^\circ \\ x+\beta+x+\alpha -x + C &=& 180^\circ \\ x+\beta +\alpha + C &=& 180^\circ \\ x+\alpha+\beta + C &=& 180^\circ \quad | \quad \mathbf{\alpha+\beta=x} \\ x+x + C &=& 180^\circ \\ 2x + C &=& 180^\circ \\ 2x &=& 180^\circ -C \quad | \quad : 2 \\ \mathbf{x} &=& \mathbf{90^\circ -\dfrac{C}{2}} \\ \hline \end{array}\\\)

Find the ordered pair \((a, b)\) of real numbers for which

\((ax + b)(x^5 + 1) - (5x + 1)\)

is divisible by \(x^{2}+1\).

\(\begin{array}{|lrcll|} \hline & P(x) &=& Q(x) (x^{2}+1) \\ & \mathbf{(ax + b)(x^5 + 1) - (5x + 1)} &=& \mathbf{Q(x) (x^{2}+1)} \\ & && \boxed{x^2+1 = 0\\ x^2 = -1\\ x=\pm i } \\ \hline x=i: & (ai + b)(i^5 + 1) - (5i + 1) &=& Q(i)\times 0 \quad | \quad i^5 = i \\ & (ai + b)(i + 1) - (5i + 1) &=& 0 \\ & (ai + b)(i + 1) - 5x - 1 &=& 0 \\ & ai^2+i(a+b-5) +b-1 &=& 0 \quad | \quad i^2 = -1 \\ & -a+i(a+b-5) +b-1 &=& 0 \\ (1) & \mathbf{-a+b-1+i(a+b-5)} &=& \mathbf{0} \\ \hline x=-i: & \left(a(-i) + b\right)\left((-i)^5 + 1\right) - \left(5(-i) + 1\right) &=& Q(-i) \times 0 \quad | \quad (-i)^5= -i \\ & (-ai + b)(-i + 1) - (-5i + 1) &=& 0 \\ & (-ai + b)(-i + 1) 5i-1 &=& 0 \\ & ai^2-i(a+b-5) +b-1 &=& 0 \quad | \quad i^2 = -1 \\ & -a-i(a+b-5) +b-1 &=& 0 \\ (2) & \mathbf{-a+b-1-i(a+b-5)} &=& \mathbf{0} \\ \hline (1)+(2):& (-a+b-1)+i(a+b-5) \\ & + (-a+b-1)-i(a+b-5)&=& 0 \\ & 2(-a+b-1) &=& 0 \\ & -a+b-1 &=& 0 \\ &\mathbf{b} &=& \mathbf{1+a} \\ \hline (1)-(2):& (-a+b-1)+i(a+b-5) \\ &- \Big( (-a+b-1)-i(a+b-5) \Big) &=& 0 \\ & (-a+b-1)+i(a+b-5) \\ & -(-a+b-1)+i(a+b-5) &=& 0 \\ & 2i(a+b-5) &=& 0 \\ & a+b-5 &=& 0 \\ &\mathbf{b} &=& \mathbf{5-a} \\ \hline &b=1+a &=& 5-a \\ & 1+a &=& 5-a \\ & 2a &=& 4 \\ & \mathbf{a} &=& \mathbf{2} \\\\ & b&=&1+a \\ & b&=&1+2 \\ & \mathbf{b} &=& \mathbf{3} \\ \hline \end{array}\)