Square ABCD has area 12.25.
E is the intersection of BD and the semicircle of diameter AD.
CF is a segment drawn from C and tangnet to the semicircle at F.
Find the area of triangle DEF.
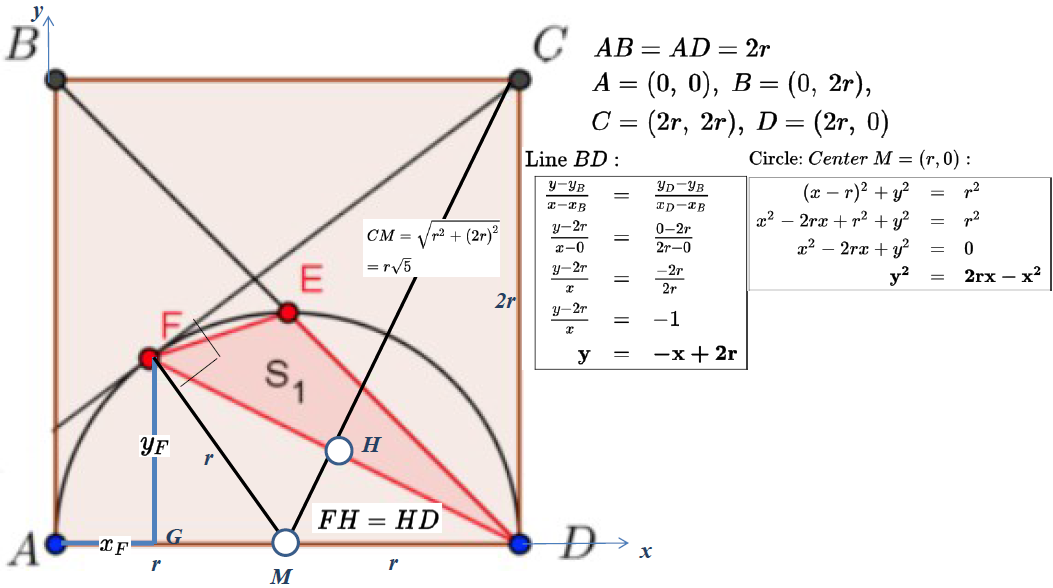
\(\begin{array}{|lll|} \hline\mathbf{Point }~E: \text{ Intersection circle and line }BD \\ \hline \begin{array}{rcll} \mathbf{y_E} &=& \mathbf{-x_E+2r} \\ \mathbf{y_E^2} &=& \mathbf{2rx_E-x_E^2} \\ (-x_E+2r)^2 &=& 2rx_E-x_E^2 \\ x_E^2 - 4rx_E+4r^2 &=& 2rx_E-x_E^2 \\ 2x_E^2-6rx_E+4r^2 &=& 0 \quad | \quad :2 \\ \mathbf{x_E^2-3rx_E+2r^2} &=& \mathbf{0} \\\\ x_E^2 &=& \dfrac{3r\pm \sqrt{9r^2-4*(2r^2)} }{2} \\ x_E^2 &=& \dfrac{3r\pm \sqrt{r^2} }{2} \\ x_E^2 &=& \dfrac{3r\pm r} {2} \\\\ x_E &=& \dfrac{3r-r}{2} \\ x_E &=& \dfrac{2r}{2} \\ \mathbf{x_E} &=& \mathbf{r}\ \checkmark \\\\ x_E &=& \dfrac{3r+r}{2} \\ x_E &=& \dfrac{4r}{2} \\ \mathbf{x_E} &=& \mathbf{2r} \quad | \quad \text{Pont }E ~\neq~ \text{Pont }D \\\\ y_E &=& -x_E+2r \quad | \quad x_E= r\\ y_E &=& -r+2r \\ \mathbf{y_E} &=& \mathbf{r}\ \checkmark \\\\ \mathbf{E} &=& \mathbf{(r,r)} \\ \end{array}\\ \hline \end{array}\)
\(\begin{array}{|rcll|} \hline \mathbf{MH}: \\ \hline r^2 &=& MH*CM \quad | \quad CM=r\sqrt{5} \\ r^2 &=& MH*r\sqrt{5} \\ r &=& MH\sqrt{5} \\ \mathbf{MH} &=& \mathbf{\dfrac{r}{\sqrt{5}} } \\ \hline \end{array}\\ \begin{array}{|rcll|} \hline \mathbf{FH}: \\ \hline FH^2 &=& MH*(CM-MH) \\ && \boxed{MH=\dfrac{r}{\sqrt{5}},\ CM=r\sqrt{5}} \\ FH^2 &=& \dfrac{r}{\sqrt{5}}*\left(r\sqrt{5}-\dfrac{r}{\sqrt{5}}\right) \\\\ FH^2 &=& r^2-\dfrac{r^2}{5} \\\\ FH^2 &=& \dfrac{4r^2}{5} \\\\ \mathbf{FH} &=& \mathbf{\dfrac{2r}{\sqrt{5}}} \\ \hline \end{array}\)
\(\begin{array}{|rcll|} \hline \mathbf{x_F}: \\ \hline FD^2 &=& (AD-x_F)*AD \quad | \quad FD=2FH,\ AD=2r \\ (2FH)^2 &=& (2r-x_F)*2r \quad | \quad FH =\dfrac{2r}{\sqrt{5}} \\ \left(\dfrac{4r}{\sqrt{5}}\right)^2 &=& (2r-x_F)*2r \\ \dfrac{16r^2}{5} &=& 4r^2-2rx_F \\ 2rx_F &=& 4r^2 - \dfrac{16r^2}{5} \quad | \quad :2r \\ x_F &=& 2r - \dfrac{8r}{5} \\ \mathbf{x_F} &=& \mathbf{\dfrac{2r}{5}} \\ \hline \end{array}\)
\(\begin{array}{|rcll|} \hline \mathbf{y_F}: \\ \hline y_F^2 &=& x_F(AD-x_F) \quad | \quad x_F=\dfrac{2r}{5},\ AD=2r \\\\ y_F^2 &=& \dfrac{2r}{5}(2r-\dfrac{2r}{5}) \\\\ y_F^2 &=& \dfrac{4r^2}{5} - \dfrac{4r^2}{25} \\\\ y_F^2 &=& \dfrac{20r^2}{5} - \dfrac{4r^2}{25} \\\\ y_F^2 &=& \dfrac{16r^2}{25} \\\\ \mathbf{y_F} &=& \mathbf{\dfrac{4r}{5}} \\ \hline \end{array}\)
\(\mathbf{F} = \mathbf{(\dfrac{2r}{5},\dfrac{4r}{5})} \)
\(\begin{array}{|lll|} \hline \mathbf{\text{The area of triangle }~DEF}: \\ \begin{array}{lccc} \hline \text{Point} & x & y & \text{cross product} \\ \hline D: & 2r & 0 \\ E: & r & r & 2r*r-r*0 \\ F: & \dfrac{2r}{5} & \dfrac{4r}{5} & r *\dfrac{4r}{5} - \dfrac{2r}{5} * r \\ D: & 2r & 0 & \dfrac{2r}{5} * 0 - 2r * \dfrac{4r}{5} \\ \hline & & & \text{sum }~=2r^2 + \dfrac{4r^2}{5} - \dfrac{2r^2}{5} - \dfrac{8r^2}{5} \\ & & & =2r^2\left(1 + \dfrac{2}{5} - \dfrac{1}{5} - \dfrac{4r}{5}\right) \\ & & & =2r^2\left(1 + \dfrac{2}{5} - 1\right) \\ & & & =2r^2\left( \dfrac{2}{5}\right) \\ & & & =\dfrac{4r^2}{5} \\ \hline \end{array}\\ \hline \end{array}\)
\(\begin{array}{|rcll|} \hline \text{The area of triangle }~DEF &=& \dfrac{\text{sum}}{2} \\\\ &=& \dfrac{\dfrac{4r^2}{5}}{2} \\\\ &=& \dfrac{2r^2}{5} \\\\ && \text{Square }~ ABCD &= AB*AD \quad | \quad AB=AD=2r \\ && \text{Square }~ ABCD &= (2r)^2 \\ && \text{Square }~ ABCD &= 4r^2 \quad | \quad \text{Square }~ ABCD= 12.25 \\ && 12.25 &= 4r^2 \quad | \quad :4 \\ && 3.0625 &= r^2 \\ && \mathbf{r^2} &= \mathbf{3.0625} \\\\ &=& \dfrac{2*3.0625}{5} \\\\ \mathbf{\text{The area of triangle }~DEF} &=& \mathbf{1.225} \\ \hline \end{array}\)
source:
https://en.wikipedia.org/wiki/Geometric_mean_theorem
https://www.youtube.com/watch?v=AByG1nTvA_Q
![]()
Square ABCD has area 12.25.
E is the intersection of BD and the semicircle of diameter AD.
CF is a segment drawn from C and tangnet to the semicircle at F.
Find the area of triangle DEF.

\(\begin{array}{|lll|} \hline\mathbf{Point }~E: \text{ Intersection circle and line }BD \\ \hline \begin{array}{rcll} \mathbf{y_E} &=& \mathbf{-x_E+2r} \\ \mathbf{y_E^2} &=& \mathbf{2rx_E-x_E^2} \\ (-x_E+2r)^2 &=& 2rx_E-x_E^2 \\ x_E^2 - 4rx_E+4r^2 &=& 2rx_E-x_E^2 \\ 2x_E^2-6rx_E+4r^2 &=& 0 \quad | \quad :2 \\ \mathbf{x_E^2-3rx_E+2r^2} &=& \mathbf{0} \\\\ x_E^2 &=& \dfrac{3r\pm \sqrt{9r^2-4*(2r^2)} }{2} \\ x_E^2 &=& \dfrac{3r\pm \sqrt{r^2} }{2} \\ x_E^2 &=& \dfrac{3r\pm r} {2} \\\\ x_E &=& \dfrac{3r-r}{2} \\ x_E &=& \dfrac{2r}{2} \\ \mathbf{x_E} &=& \mathbf{r}\ \checkmark \\\\ x_E &=& \dfrac{3r+r}{2} \\ x_E &=& \dfrac{4r}{2} \\ \mathbf{x_E} &=& \mathbf{2r} \quad | \quad \text{Pont }E ~\neq~ \text{Pont }D \\\\ y_E &=& -x_E+2r \quad | \quad x_E= r\\ y_E &=& -r+2r \\ \mathbf{y_E} &=& \mathbf{r}\ \checkmark \\\\ \mathbf{E} &=& \mathbf{(r,r)} \\ \end{array}\\ \hline \end{array}\)
\(\begin{array}{|rcll|} \hline \mathbf{MH}: \\ \hline r^2 &=& MH*CM \quad | \quad CM=r\sqrt{5} \\ r^2 &=& MH*r\sqrt{5} \\ r &=& MH\sqrt{5} \\ \mathbf{MH} &=& \mathbf{\dfrac{r}{\sqrt{5}} } \\ \hline \end{array} \begin{array}{|rcll|} \hline \mathbf{FH}: \\ \hline FH^2 &=& MH*(CM-MH) \\ && \boxed{MH=\dfrac{r}{\sqrt{5}},\ CM=r\sqrt{5}} \\ FH^2 &=& \dfrac{r}{\sqrt{5}}*\left(r\sqrt{5}-\dfrac{r}{\sqrt{5}}\right) \\\\ FH^2 &=& r^2-\dfrac{r^2}{5} \\\\ FH^2 &=& \dfrac{4r^2}{5} \\\\ \mathbf{FH} &=& \mathbf{\dfrac{2r}{\sqrt{5}}} \\ \hline \end{array}\)
\(\begin{array}{|rcll|} \hline \mathbf{x_F}: \\ \hline FD^2 &=& (AD-x_F)*AD \quad | \quad FD=2FH,\ AD=2r \\ (2FH)^2 &=& (2r-x_F)*2r \quad | \quad FH =\dfrac{2r}{\sqrt{5}} \\ \left(\dfrac{4r}{\sqrt{5}}\right)^2 &=& (2r-x_F)*2r \\ \dfrac{16r^2}{5} &=& 4r^2-2rx_F \\ 2rx_F &=& 4r^2 - \dfrac{16r^2}{5} \quad | \quad :2r \\ x_F &=& 2r - \dfrac{8r}{5} \\ \mathbf{x_F} &=& \mathbf{\dfrac{2r}{5}} \\ \hline \end{array} \)
\(\begin{array}{|rcll|} \hline \mathbf{y_F}: \\ \hline y_F^2 &=& x_F(AD-x_F) \quad | \quad x_F=\dfrac{2r}{5},\ AD=2r \\\\ y_F^2 &=& \dfrac{2r}{5}(2r-\dfrac{2r}{5}) \\\\ y_F^2 &=& \dfrac{4r^2}{5} - \dfrac{4r^2}{25} \\\\ y_F^2 &=& \dfrac{20r^2}{5} - \dfrac{4r^2}{25} \\\\ y_F^2 &=& \dfrac{16r^2}{25} \\\\ \mathbf{y_F} &=& \mathbf{\dfrac{4r}{5}} \\ \hline \end{array}\)
\(\mathbf{F} = \mathbf{(\dfrac{2r}{5},\dfrac{4r}{5})} \)
\(\begin{array}{|lll|} \hline \mathbf{\text{The area of triangle }~DEF}: \\ \begin{array}{lccc} \hline \text{Point} & x & y & \text{cross product} \\ \hline D: & 2r & 0 \\ E: & r & r & 2r*r-r*0 \\ F: & \dfrac{2r}{5} & \dfrac{4r}{5} & r *\dfrac{4r}{5} - \dfrac{2r}{5} * r \\ D: & 2r & 0 & \dfrac{2r}{5} * 0 - 2r * \dfrac{4r}{5} \\ \hline & & & \text{sum }~=2r^2 + \dfrac{4r^2}{5} - \dfrac{2r^2}{5} - \dfrac{8r^2}{5} \\ & & & =2r^2\left(1 + \dfrac{2}{5} - \dfrac{1}{5} - \dfrac{4r}{5}\right) \\ & & & =2r^2\left(1 + \dfrac{2}{5} - 1\right) \\ & & & =2r^2\left( \dfrac{2}{5}\right) \\ & & & =\dfrac{4r^2}{5} \\ \hline \end{array}\\ \hline \end{array} \)
\(\begin{array}{|rcll|} \hline \text{The area of triangle }~DEF &=& \dfrac{\text{sum}}{2} \\\\ &=& \dfrac{\dfrac{4r^2}{5}}{2} \\\\ &=& \dfrac{2r^2}{5} \\\\ && \text{Square }~ ABCD &= AB*AD \quad | \quad AB=AD=2r \\ && \text{Square }~ ABCD &= (2r)^2 \\ && \text{Square }~ ABCD &= 4r^2 \quad | \quad \text{Square }~ ABCD= 12.25 \\ && 12.25 &= 4r^2 \quad | \quad :4 \\ && 3.0625 &= r^2 \\ && \mathbf{r^2} &= \mathbf{3.0625} \\\\ &=& \dfrac{2*3.0625}{5} \\\\ \mathbf{\text{The area of triangle }~DEF} &=& \mathbf{1.225} \\ \hline \end{array}\)
Source: https://en.wikipedia.org/wiki/Geometric_mean_theorem
https://www.youtube.com/watch?v=AByG1nTvA_Q
![]()
Given that triangle ABCAis an irregular triangle, AD is the median which bisects BC, and the green, blue and red regions are squares.
If the total area of green region and blue region is 9, find the area of the red region.
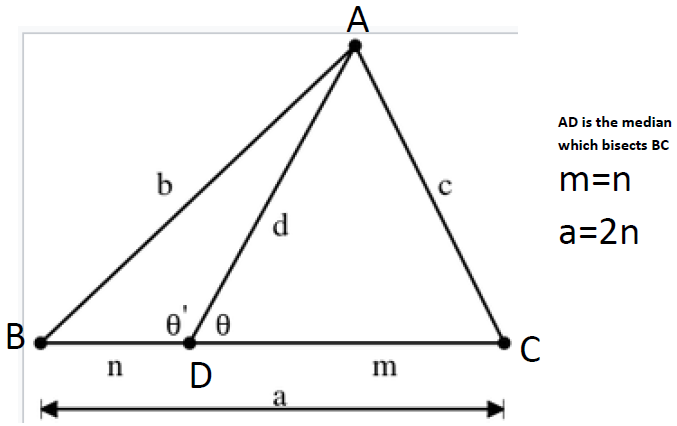
\(b^2m+c^2n=a(d^2+mn)\)
Source: https://en.wikipedia.org/wiki/Cevian#Ratio_properties
\(\begin{array}{|rcll|} \hline b^2m+c^2n &=& a(d^2+mn) \quad | \quad m=n, a=2n \\ b^2n+c^2n &=& 2n(d^2+n^2) \\ (b^2+c^2)n &=& 2n(d^2+n^2) \\ {\color{red}b^2}+{\color{red}c^2} &=& 2({\color{blue}d^2}+{\color{green}n^2}) \\ {\color{red}b^2}+{\color{red}c^2} &=& 2*9 \\ \mathbf{{\color{red}b^2}+{\color{red}c^2}} &=& \mathbf{18} \\ \hline \end{array}\)
The area of the red region is 18
![]()