heureka

Thank you, CPhill !

Thank you, CPhill !

In the diagram below,
we have \(\angle PQR = \angle PRQ = \angle STR = \angle RST\), \(QR = 8\), and \(QS = 2\).
Find PQ.

\(\text{Let PQ = x }\)

\(\begin{array}{|rcll|} \hline \text{In $\triangle PQR$}: \\ \hline \mathbf{\dfrac{\sin(180^\circ-2A)}{8}} &=& \mathbf{\dfrac{\sin(A)}{x}} \\\\ \dfrac{\sin(2A)}{8} &=& \dfrac{\sin(A)}{x} \\\\ \dfrac{2\sin(A)\cos(A)}{8} &=& \dfrac{\sin(A)}{x} \\\\ \dfrac{2\cos(A)}{8} &=& \dfrac{1}{x} \\\\ \dfrac{\cos(A)}{4} &=& \dfrac{1}{x} \\\\ \dfrac{4}{\cos(A)} &=& x \\\\ \mathbf{x} &=& \mathbf{\dfrac{4}{\cos(A)}} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \text{In $\triangle SQR$}: \\ \hline \mathbf{\dfrac{\sin(3A-180^\circ)}{2}} &=& \mathbf{\dfrac{\sin(180^\circ-A)}{8}} \\\\ \dfrac{\sin\Big(-(180^\circ-3A)\Big)}{2} &=& \dfrac{\sin(A)}{8} \\\\ \dfrac{-\sin(180^\circ-3A)}{2} &=& \dfrac{\sin(A)}{8} \\\\ \dfrac{-\sin(3A)}{2} &=& \dfrac{\sin(A)}{8} \\\\ -\sin(3A) &=& \dfrac{\sin(A)}{4} \small{ \begin{array}{|rcll|} \hline && \mathbf{\sin(3A)} \\ &=&\sin(2A)\cos(A)+\cos(2A)\sin(A)\\ &=&2\sin(A)\cos(A)\cos(A)+\Big(\cos^2(A)-\sin^2(A)\Big)\sin(A) \\ &=&2\sin(A)\cos^2(A)+\Big(\cos^2(A)-\sin^2(A)\Big)\sin(A) \\ &=&2\sin(A)\cos^2(A)+\Big(\cos^2(A)-(1-\cos^2(A))\Big)\sin(A) \\ &=&2\sin(A)\cos^2(A)+\Big(2\cos^2(A)-1\Big)\sin(A) \\ &=&\sin(A)\Bigg( 2\cos^2(A)+\Big(2\cos^2(A)-1\Big) \Bigg) \\ &=&\mathbf{\sin(A)\Big( 4\cos^2(A)-1\Big)} \\ \hline \end{array} } \\\\ -\sin(A)\Big( 4\cos^2(A)-1\Big) &=& \dfrac{\sin(A)}{4} \\ - \Big( 4\cos^2(A)-1\Big) &=& \dfrac{1}{4} \\ -4\cos^2(A)+1 &=& \dfrac{1}{4} \quad | \quad * (-4) \\ 16\cos^2(A)-4 &=& -1 \\ 16\cos^2(A) &=& 3 \quad | \quad \sqrt{()} \\ 4\cos(A) &=& \sqrt{3} \\ \mathbf{\cos(A)} &=& \mathbf{\dfrac{\sqrt{3}}{4}} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{x} &=& \mathbf{\dfrac{4}{\cos(A)}} \\\\ x &=& \dfrac{4}{\dfrac{\sqrt{3}}{4}} \\\\ \mathbf{x} &=& \mathbf{\dfrac{16}{ \sqrt{3} } } \\ \hline \end{array}\)

PQ \(= \mathbf{\dfrac{16}{ \sqrt{3} } = 9.23760430703 }\)

The expression \(\cos(x) + \cos(3x) + \cos(7x) + \cos(9x)\) can be written in the equivalent form \(a \cos(bx)\cos(cx)\cos(dx)\)

for some positive integers \(a\), \(b\), \(c\), and \(d\).

Find \(a + b + c + d\).

Formula:

\(\boxed{\cos(x)+\cos(y)=2\cos\left(\dfrac{x+y}{2}\right)\cos\left(\dfrac{x-y}{2}\right) }\)

\(\begin{array}{|rcll|} \hline && \mathbf{\cos(x) + \cos(3x) + \cos(7x) + \cos(9x)} \\\\ &=& \Big(\cos(9x) + \cos(x)\Big) + \Big(\cos(7x) + \cos(3x)\Big) \\\\ &=& 2\cos\left(\dfrac{9x+x}{2}\right)\cos\left(\dfrac{9x-x}{2}\right) + 2\cos\left(\dfrac{7x+3x}{2}\right)\cos\left(\dfrac{7x-3x}{2}\right) \\\\ &=& 2\cos\left(\dfrac{10}{2}x\right)\cos\left(\dfrac{8}{2}x\right) + 2\cos\left(\dfrac{10}{2}x\right)\cos\left(\dfrac{4}{2}x\right) \\\\ &=& 2\cos(5x)\cos(4x) + 2\cos(5x)\cos(2x) \\\\ &=& 2\cos(5x)\Big(\cos(4x) + \cos(2x)\Big) \\\\ &=& 2\cos(5x)*2\cos\left(\dfrac{4x+2x}{2}\right)\cos\left(\dfrac{4x-2x}{2}\right) \\\\ &=& 4\cos(5x)\cos\left(\dfrac{6}{2}x\right)\cos\left(\dfrac{2}{2}x\right) \\\\ &=&\mathbf{ 4\cos(5x)\cos(3x)\cos(x) } \qquad a=4,\ b=5,\ c=3,\ d=1 \\ \hline && \mathbf{a+b+c+d } \\ &=& 4+5+3+1 \\ &=& \mathbf{13} \\ \hline \end{array}\)

A regular dodecahedron \(P_1 P_2 P_3 \dotsb P_{12}\) is inscribed in a circle with radius 1.
Compute  \((P_1 P_2)^2 + (P_1 P_3)^2 + \dots + (P_{11} P_{12})^2\).
(The sum includes all terms of the form \((P_i P_j)^2\), where \(1 \le i < j \le 12\).

The \((P_1 P_2)\) isn't multiplication, it shows the distance from point one to two.

A square is inscribed in a right triangle, as shown below.

The legs of the triangle are 2 and 3. 

Find the side length of the square.

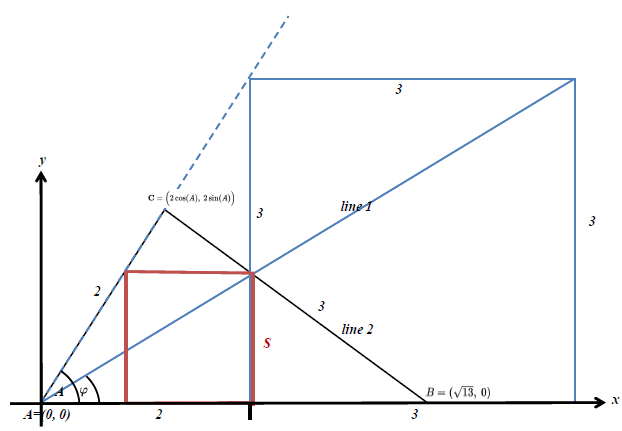
\(\text{Let $A=(0,\ 0)$ } \\ \text{Let $B=(x_b,\ y_b)=(\sqrt{13},\ 0)$ } \\ \text{Let $C=(x_c,\ y_c)=\Big(2\cos(A),\ 2\sin(A)\Big)$ } \\ \text{Let $ \cos(A)=\dfrac{2}{\sqrt{13}},\ \sin(A)=\dfrac{3}{\sqrt{13}}$ } \)

\(\begin{array}{|lrcll|} \hline & \tan{\varphi} &=& \dfrac{2}{2+3} \\\\ & \tan{\varphi} &=& \dfrac{2}{5} \\\\ \text{line }1: & y &=& \tan{\varphi}*x \\\\ & \mathbf{y} &=& \mathbf{\dfrac{2}{5}*x} \\ \\ \hline \text{line }2: & \dfrac{y-y_b}{x-x_b} &=& \dfrac{y_c-y_b}{x_c-x_b} \\\\ &&& \boxed{x_b=\sqrt{13},\ y_b = 0,\quad x_c=\dfrac{4}{\sqrt{13}},\ y_c = \dfrac{6}{\sqrt{13}} } \\\\ & \dfrac{y}{x-\sqrt{13}} &=& \dfrac{\dfrac{6}{\sqrt{13}}}{\dfrac{4}{\sqrt{13}}-\sqrt{13}} \\\\ & \dfrac{y}{x-\sqrt{13}} &=& \dfrac{6}{4-13} \\\\ & \dfrac{y}{x-\sqrt{13}} &=& -\dfrac{2}{3} \\\\ & \mathbf{y} &=& \mathbf{-\dfrac{2}{3}(x-\sqrt{13})} \\ \hline \end{array}\)

The intersection point of both lines:

\(\begin{array}{|rcll|} \hline y= \dfrac{2}{5}*x &=& -\dfrac{2}{3}(x-\sqrt{13}) \\\\ \dfrac{2}{5}*x &=& -\dfrac{2}{3}(x-\sqrt{13}) \\\\ \dfrac{9}{10}*x &=& -(x-\sqrt{13}) \\\\ \dfrac{9}{10}*x &=& -x+\sqrt{13} \\\\ x+ \dfrac{9}{10}*x &=& \sqrt{13} \\\\ \dfrac{19}{10}*x &=& \sqrt{13} \\\\ x &=& \dfrac{10\sqrt{13}}{19} \\\\ y = s &=& \dfrac{3}{5}x \\\\ s &=& \dfrac{3}{5}*\dfrac{10\sqrt{13}}{19} \\\\ s &=& \dfrac{6}{19} \sqrt{13} \\ \mathbf{s} &=& \mathbf{1.13859513962} \\ \hline \end{array}\)

The side length of the square is \(\mathbf{\dfrac{6}{19} \sqrt{13} = 1.13859513962}\)

364 is a multiple of 7 but not a multiple of 3 384 is a multiple of 3 but not a multiple of 7

Find a number between 364 and 384 that is both a multiple of 7 and a multiple of 3

\(378=2*3^3*7\)

7 t-shirts and a hat costs £67.00

5 t-shirts and a hat costs £49.00.

How much does a t-shirt cost?

How much does a hat cost?

Let t-shirt \(= x \)
Let hat \(= y\)

\(\begin{array}{|lrcll|} \hline (1) & 7x+y &=& 67 \\ (2) & 5x+y &=& 49 \\ \hline (1)-(2): & 7x+y -(5x+y) &=& 67-49 \\ & 7x+y -5x -y &=& 18 \\ & 7x -5x &=& 18 \\ & 2x &=& 18 \quad | \quad :2 \\ & \mathbf{x} &=& \mathbf{9} \\ \hline & 5x+y &=& 49 \quad | \quad \mathbf{x=9} \\ & 5*9+y &=& 49 \\ & 45 + y &=& 49 \\ & y &=& 49-45 \\ & \mathbf{y} &=& \mathbf{4} \\ \hline \end{array}\)

A t-shirt does \(\mathbf{£9.00}\) cost?
A hat does \(\mathbf{£4.00}\) cost?

A manager wants to assign 20 workers to four distinct construction jobs.
These jobs require 6, 4, 3, and 7 workers respectively.
In how many different ways can the manager assign the workers?

\(\text{Let Job$_1 = a$} \\ \text{Let Job$_2 = b$} \\ \text{Let Job$_3 = c$} \\ \text{Let Job$_4 = d$} \\ \text{The word is $\mathbf{aaaaaabbbbcccddddddd}$ (The word-length is $20$ ),$\\$how many differnet words we can have ?}\)

multinomial coefficient:

\(\begin{array}{|rcll|} \hline \dfrac{20!}{6!\ 4!\ 3!\ 7!} &=& 4655851200 \\ \hline \end{array}\)

In 4655851200 different ways can the manager assign the workers.