heureka

If

\(ab = 15\) and \(a^2 + b^2 = 40\), then find the value of \((a + b)^4 - (a - b)^4\).

\(\begin{array}{|rcll|} \hline \mathbf{(a + b)^4 - (a - b)^4} &=& \left((a + b)^2\right)^2 - \left((a - b)^2\right)^2 \\ &=& \left(a^2+2ab+b^2\right)^2 - \left(a^2-2ab+b^2\right)^2 \\ &=& \left(a^2+b^2+2ab\right)^2 - \left(a^2+b^2-2ab\right)^2 \\ &=& \left(40+2*15\right)^2 - \left(40-2*15\right)^2 \\ &=& 70^2 - 10^2 \\ &=& 4900-100 \\ &=& \mathbf{4800} \\ \hline \end{array}\)

Simplify 

\(\dfrac{\sin (A-B)}{\sin A \sin B} + \dfrac{\sin (B-C)}{\sin B \sin C} + \dfrac{\sin (C-A)}{\sin C \sin A}\)

\(\begin{array}{|rcll|} \hline && \mathbf{\dfrac{\sin(A-B)}{\sin A \sin B} + \dfrac{\sin(B-C)}{\sin B \sin C} + \dfrac{\sin(C-A)}{\sin C \sin A} } \\\\ &=& \dfrac{\sin(A)\cos(B)-\cos(A)\sin(B)}{\sin A \sin B} + \dfrac{\sin(B)\cos(C)-\cos(B)\sin(C)}{\sin B \sin C} + \dfrac{\sin(C)\cos(A)-\cos(C)\sin(A)}{\sin C \sin A} \\\\ &=& \dfrac{\sin(A)\cos(B)}{\sin A \sin B}-\dfrac{\cos(A)\sin(B)}{\sin A \sin B} + \dfrac{\sin(B)\cos(C)}{\sin B \sin C}-\dfrac{\cos(B)\sin(C)}{\sin B \sin C} + \dfrac{\sin(C)\cos(A)}{\sin C \sin A}-\dfrac{\cos(C)\sin(A)}{\sin C \sin A} \\\\ &=& \dfrac{\cos(B)}{\sin B}-\dfrac{\cos(A)}{\sin A} + \dfrac{\cos(C)}{\sin C}-\dfrac{\cos(B)}{\sin B} + \dfrac{\cos(A)}{\sin A}-\dfrac{\cos(C)}{\sin C} \\\\ &=& \dfrac{\cos(B)}{\sin B}-\dfrac{\cos(B)}{\sin B} + \dfrac{\cos(C)}{\sin C}-\dfrac{\cos(C)}{\sin C} + \dfrac{\cos(A)}{\sin A}-\dfrac{\cos(A)}{\sin A} \\\\ &=& \mathbf{0} \\ \hline \end{array}\)

have got 100 lamp bulbs with 100 switches. Initially all switches are turned off.

After that I change the position of each switch. After that I change the position of each second, third, fourth... hundredth switch.

How many bulbs will light up?

I assume:

All lamps will light up on a perfect square position:  {1,4,9,16,25,36,49,64,81,100} = 10 lamps will light up.

What is the remainder when \(7^{42}\) is divided by \(16\)?

\(\begin{array}{|rcll|} \hline && 7^{42} \pmod{16} \quad | \quad 7^2 \pmod{16} = 1 \\ &\equiv& 7^{2*21} \pmod{16} \\ &\equiv& \left(7^{2}\right)^{21} \pmod{16} \\ &\equiv& \left(1\right)^{21} \pmod{16} \\ &\equiv& \mathbf{1} \pmod{16} \\ \hline \end{array} \)

The remainder is \(\mathbf{1}\)

ABCD is a rhombus with ∠B=60∘, ∠APC=120∘, BP=3 and PD=2.

Find the difference between the lengths of AP and PC.

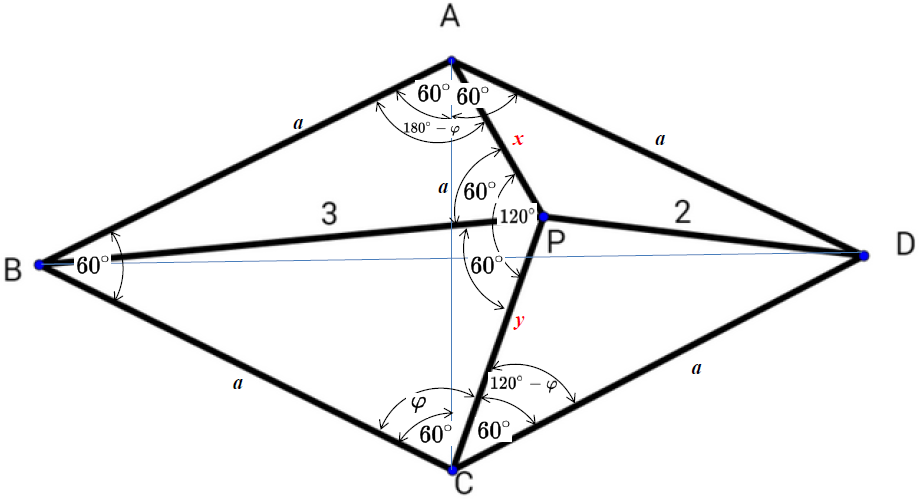
\(\text{LET $AC=a\qquad$ (equilateral triangle) $ABC$} \\ \text{LET $BD=f$} \\ \text{LET $AP=x$} \\ \text{LET $PC=y$} \\ \text{LET $\angle PCA = \varphi-60^\circ$} \\ \text{LET $\angle CAP = 180^\circ-\varphi$}\)

cos-rule:

\(\begin{array}{|rcll|} \hline \text{In $\triangle ABD$} \\ \cos(120^\circ)=-\frac{1}{2} \\ \hline f^2 &=&a^2+a^2-2aa\cos(120^\circ) \\ f^2 &=& 2a^2(1-\cos(120^\circ)) \\ f^2 &=& 2a^2(1+\dfrac{1}{2}) \\ \ldots \\ \mathbf{f} &=& \mathbf{a\sqrt{3}} \\ \hline \end{array} \begin{array}{|rcll|} \hline \text{In $\triangle ACP$} \\ \cos(120^\circ)=-\frac{1}{2} \\ \hline a^2 &=&x^2+y^2-2xy\cos(120^\circ) \\ \mathbf{a^2} &=& \mathbf{x^2+y^2+xy} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \dfrac{\sin(\varphi)}{3} &=& \dfrac{\sin(\angle BPC)}{a} \\\\ \dfrac{180^\circ-\sin(\varphi)}{3} &=& \dfrac{\sin(\angle BPA)}{a} \\ \dfrac{\sin(\varphi)}{3} &=& \dfrac{\sin(\angle BPA)}{a} \\\\ \hline \dfrac{\sin(\varphi)}{3} = \dfrac{\sin(\angle BPC)}{a} &=& \dfrac{\sin(\angle BPA)}{a} \\ \dfrac{sin(\angle BPC)}{a} &=& \dfrac{\sin(\angle BPA)}{a} \\\\ \angle BPC &=& \angle BPA \quad | \quad \angle BPC+\angle BPA=120^\circ \\ \angle BPC &=& \angle BPA = \dfrac{120^\circ}{2} \\ \mathbf{\angle BPC} &=& \mathbf{\angle BPA = 60^\circ } \\ \hline \end{array}\)

Formula:

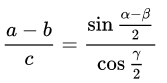
\(\begin{array}{|rcll|} \hline \text{In $\triangle APC$} \\ \hline \dfrac{y-x}{a} &=& \dfrac{ \sin\left( \dfrac{(120^\circ-\varphi)-(\varphi-60^\circ) } {2} \right) } { \cos\left(\dfrac{120^\circ}{2}\right) } \\\\ \dfrac{y-x}{a} &=& \dfrac{ \sin\left( \dfrac{180^\circ-2\varphi } {2} \right) } { \cos(60^\circ) } \\\\ \dfrac{y-x}{a} &=& \dfrac{ \sin(90^\circ-\varphi ) } { \cos(60^\circ) } \\\\ \dfrac{y-x}{a} &=& \dfrac{ \cos(\varphi) } { \cos(60^\circ) } \quad | \quad \cos(60^\circ ) = \frac{1}{2} \\\\ \dfrac{y-x}{a} &=& 2\cos(\varphi) \\\\ \mathbf{y-x} &=& \mathbf{2a\cos(\varphi)} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \text{In $\triangle ABP$} \\ \cos(60^\circ)=\frac{1}{2} \\ \hline a^2 &=& x^2+3^2-2*3x\cos(60^\circ) \\ \mathbf{a^2} &=& \mathbf{x^2+9-3x} \qquad (1) \\ \hline \end{array} \begin{array}{|rcll|} \hline \text{In $\triangle BCP$} \\ \cos(60^\circ)=\frac{1}{2} \\ \hline a^2 &=& y^2+3^2-2*3y\cos(60^\circ) \\ \mathbf{a^2} &=& \mathbf{y^2+9-3y} \qquad (2) \\ \hline \end{array} \)

\(\begin{array}{|lrcll|} \hline (1)-(2): & 0 &=& x^2+9-3x-(y^2+9-3y) \\ & 0 &=& x^2+9-3x-y^2-9+3y \\ & 0 &=& x^2-y^2-3x+3y \\ & 0 &=& (x-y)(x+y)-3(x-y) \\ & 3(x-y) &=& (x-y)(x+y) \quad | \quad :(x-y) \qquad (x-y) \ne 0 ! \qquad x\ne y \\ & 3 &=& x+y \\ & \mathbf{x+y} &=& \mathbf{3} \\ \hline \end{array}\)

cos-rule:

\(\begin{array}{|rcll|} \hline \text{In $\triangle CDP$} \\ \cos(120^\circ)=-\frac{1}{2} \\ \sin(120^\circ)=\frac{\sqrt{3}}{2} \\ \sin(60^\circ)=\frac{\sqrt{3}}{2} \\ \hline 2^2&=& y^2+a^2-2ay\cos(120^\circ-\varphi) \\ 2ay\cos(120^\circ-\varphi) &=& y^2+a^2 -4 \\ \cos(120^\circ-\varphi) &=& \dfrac{y^2+a^2 -4} {2ay} \\ \cos(120^\circ)\cos(\varphi)+\sin(120^\circ)\sin(\varphi) &=& \dfrac{y^2+a^2 -4} {2ay} \\ -\dfrac{\cos(\varphi)}{2}+\dfrac{\sqrt{3}}{2}\sin(\varphi) &=& \dfrac{y^2+a^2 -4} {2ay} \\ && \text{In $\triangle BCP$}:\\ && \boxed{\dfrac{\sin(\varphi)}{3}= \dfrac{\sin(60^\circ)}{a} \\ \sin(\varphi) = \dfrac{3}{a}*\dfrac{\sqrt{3}}{2} } \\ -\dfrac{\cos(\varphi)}{2}+\dfrac{\sqrt{3}}{2}*\dfrac{3}{a}*\dfrac{\sqrt{3}}{2} &=& \dfrac{y^2+a^2 -4} {2ay} \\ \dfrac{9}{4a}-\dfrac{\cos(\varphi)}{2} &=& \dfrac{y^2+a^2 -4} {2ay} \\ \dfrac{9}{2a}-\cos(\varphi) &=& \dfrac{y^2+a^2 -4} {ay} \\ \mathbf{\cos(\varphi)} &=& \mathbf{\dfrac{9}{2a} - \dfrac{y^2+a^2 -4} {ay}} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{\cos(\varphi)} &=& \mathbf{\dfrac{9}{2a} - \dfrac{y^2+a^2 -4} {ay}} \\ \hline \mathbf{y-x} &=& \mathbf{2a\cos(\varphi)} \\ y-x &=& 2a\left( \dfrac{9}{2a} - \dfrac{(y^2+a^2 -4)} {ay}*\dfrac{2}{2} \right) \\ y-x &=& \dfrac{2a}{2a}\left( 9 - \dfrac{2(y^2+a^2 -4)} {y} \right) \\ y-x &=& 9 - \dfrac{2(y^2+a^2 -4)} {y} \\ y-x &=& \dfrac{9y-2(y^2+a^2 -4)} {y} \\ y-x &=& \dfrac{9y-(2y^2+2a^2 -8)} {y} \quad | \quad a^2 = y^2+9-3y \\ y-x &=& \dfrac{9y-\Big(2y^2+2(y^2+9-3y) -8 \Big)} {y} \\ y-x &=& \dfrac{9y-(4y^2-6y+10) } {y} \\ y-x &=& \dfrac{15y-4y^2-10} {y} \\ y(y-x) &=& 15y-4y^2-10 \quad | \quad \mathbf{x+y=3}\ \text{or}\ x=3-y \\ y\Big(y-(3-y)\Big) &=& 15y-4y^2-10 \\ y(2y-3) &=& 15y-4y^2-10 \\ 2y^2-3y &=& 15y-4y^2-10 \\\\ \mathbf{6y^2 -18y +10} &=& \mathbf{0} \\ y &=& \dfrac{18\pm \sqrt{18^2-4*6*10}}{2*6} \\\\ y &=& \dfrac{18\pm \sqrt{84} } {12} \\\\ y &=& \dfrac{18+ \sqrt{84} }{12} \\\\ y &=& \dfrac{18+ \sqrt{84} }{12} \\\\ \mathbf{y} &=& \mathbf{2.26376261583} \\\\ x &=& 3-y \\ x &=& 3- 2.26376261583 \\ \mathbf{x} &=& \mathbf{0.73623738417} \\\\ x-y &=& 0.73623738417 - 2.26376261583 \\ \mathbf{x-y} &=& \mathbf{-1.52752523165} \\ \hline \end{array}\)

The difference between the lengths of AP and PC is \(\mathbf{-1.52752523165}\)

In triangle \(XYZ\), \(XY = XZ\).  \(W\) is on side \(XZ \) so that \(XW = WY = YZ\).

Find \(\angle XYW\).

\(\text{Let $\angle XYW=x$} \)

\(\begin{array}{|rcll|} \hline y &=& \dfrac{180^\circ-x}{2} \\ \mathbf{y} &=& \mathbf{90^\circ-\dfrac{x}{2}} \\ \hline \end{array} \)

\(\begin{array}{|rcll|} \hline \text{In }\triangle YWZ \\ \hline 180^\circ &=& y + y + (y-x) \\ 180^\circ &=& 3y -x \quad | \quad \mathbf{y=90^\circ-\dfrac{x}{2}} \\ 180^\circ &=& 3\left(90^\circ-\dfrac{x}{2} \right)-x \\ 180^\circ &=& 270^\circ-\dfrac{3x}{2} -x \\ 180^\circ &=& 270^\circ-\dfrac{5x}{2} \\ \dfrac{5x}{2} &=& 270^\circ-180^\circ \\ \dfrac{5x}{2} &=& 90^\circ \\ x &=& \dfrac{2*90^\circ}{5} \\ x &=& 2*18^\circ \\ \mathbf{x} &=& \mathbf{36^\circ} \\ \hline \end{array}\)

A rectangular sheet PQRS is such that PQ = 6 and QR = 8.  It is folded so that corner P goes to corner R. 

Find the length of the crease.

\(\begin{array}{|rclrclrcl|} \hline \tan(\psi) &=& \dfrac{6}{8} & &=& & \tan(\psi) &=& \dfrac{x}{\sqrt{6^2+8^2}} \\\\ && &\dfrac{6}{8} &=& \dfrac{x}{\sqrt{6^2+8^2}} \\\\ && &\dfrac{6}{8} &=& \dfrac{x}{10} \\\\ && & x &=& \dfrac{6*10}{8} \\\\ && & x &=& \dfrac{60}{8} \\\\ &&& \mathbf{x} &=& \mathbf{7.5 } \\ \hline \end{array}\)

The length of the crease is \(\mathbf{7.5 }\)

For a positive integer \(n\), the n^{th} triangular number is \(T(n)=\dfrac{n(n+1)}{2}\).
For example, \(T(3) = \frac{3(3+1)}{2}= \frac{3(4)}{2}=6\), so the third triangular number is \(6\).
Determine the smallest integer \(b>2011\) such that \(T(b+1)-T(b)=T(x)\) for some positive integer \(x\).

My attempt:

\(\begin{array}{|rcll|} \hline \mathbf{T(b+1)-T(b)} &=& \mathbf{T(x)} \\\\ \dfrac{(b+1)(b+1+1)}{2}-\dfrac{b(b+1)}{2} &=& \dfrac{x(x+1)}{2} \\\\ (b+1)(b+2)-b(b+1) &=& x(x+1) \\ (b+1)(b+2-b) &=& x(x+1) \\ 2(b+1) &=& x(x+1) \\ b+1 &=& \dfrac{x(x+1)}{2} \\ b+1 &=& T(x) \\ \mathbf{b} &=& \mathbf{T(x)-1} \qquad (1) \\ \hline \end{array} \)

\(\begin{array}{|lrcll|} \hline (1) & \mathbf{T(x)-1} &=& \mathbf{b} \quad | \quad b > 2011 \\ & T(x)-1 &\mathbf{>}& 2011 \\ & T(x) &\mathbf{>}& 2012 \\ & \dfrac{x(x+1)}{2}&\mathbf{>}& 2012 \\ & x(x+1) &\mathbf{>}& 4024 \\ & x^2+x &\mathbf{>}& 4024 \\ & x^2+x-4024 &\mathbf{>}& 0 \\\\ & \mathbf{x^2+x-4024} &=& \mathbf{0} \\\\ & x &=& \dfrac{-1+\sqrt{1-4(-4024)} }{2} \\ & x &=& \dfrac{-1+\sqrt{16097} }{2} \\ & x &=& \dfrac{-1+126.873953198}{2} \\ & x &=& \dfrac{125.873953198}{2} \\ & x &=& 62.9369765988 \\\\ & x &\mathbf{>}& 62.9369765988 \quad (\text{positive integer }x ) \\ & \mathbf{x} &=& \mathbf{63} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline T(63) &=& \dfrac{63(63+1)}{2} \\\\ T(63) &=& \dfrac{63*64}{2} \\\\ \mathbf{T(63)} &=& \mathbf{2016} \\ \hline \end{array} \begin{array}{|rcll|} \hline \mathbf{b} &=& \mathbf{T(x) - 1} \quad | \quad x = 63 \\ b &=& T(63) - 1 \\ b &=& 2016 - 1 \\ \mathbf{b} &=& \mathbf{2015} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{T(b+1)} &=& \mathbf{ \dfrac{(b+1)(b+2)}{2} } \quad | \quad b = 2015 \\\\ T(2015+1) &=& \dfrac{(2015+1)(2015+2)}{2} \\\\ T(2016) &=& \dfrac{2016*2017}{2} \\\\ \mathbf{T(2016)} &=& \mathbf{2033136} \\ \hline \end{array} \begin{array}{|rcll|} \hline \mathbf{T(b)} &=& \mathbf{ \dfrac{b(b+1)}{2} } \quad | \quad b = 2015 \\\\ T(2015) &=& \dfrac{2015(2015+1)}{2} \\\\ T(2016) &=& \dfrac{2015*2016}{2} \\\\ \mathbf{T(2015)} &=& \mathbf{2031120} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{T(b+1)-T(b)} &=& \mathbf{T(x)} \qquad b > 2011 \\ T(b+1)-T(b) &=& T(x) \quad | \quad b=2015,\ x = 63 \\ T(2016)-T(2015) &=& T(63) \quad | \quad \mathbf{T(2016)=2033136},\ \mathbf{T(2015)=2031120} \\ 2033136-2031120 &=& 2016\ \checkmark \\ \hline \end{array}\)

Sausages come in packets of 6.
Bread rolls come in packets of 8.
Brian wants to buy enough packs of sausages and rolls so that there are an equal number of sausages and rolls.
What is the minimum number of sausages and rolls he needs to buy?

\(lcm(6,8) = 24 \)

packets of Sausages \(= \dfrac{24}{6} = 4\)
packets of Bread rolls \(= \dfrac{24}{8} = 3\)

Find the angle between the hour hand and minute hand of a clock when it is 9:20.

\(\begin{array}{rcll} \Delta\alpha^{\circ} &=& 330 \times t^h \pmod{360^{\circ}} \quad | \quad \mathbf{t^h=9+\dfrac{20}{60} = \dfrac{28}{3}\ h } \\ &=& 330 \times \dfrac{28}{3} \pmod{360^{\circ}} \\ &=& 3080^{\circ} \pmod{360^{\circ}} \\ &=& \mathbf{200^{\circ}} \qquad (\text{greater angle)} \\ &=& \mathbf{360^\circ-200^{\circ}=160^\circ} \qquad (\text{smaller angle)} \\ \end{array} \)