heureka

Express
\(\left(\dfrac{1}{2} + \dfrac{\sqrt{3}}{2}i\right)^{2015}\)
in the form a + bi.

\(\begin{array}{|rcll|} \hline \varphi &=& \arctan\left( \dfrac{\dfrac{\sqrt{3}}{2}}{\dfrac{1}{2}} \right) \\ \varphi &=& \arctan(\sqrt{3}) \\ \mathbf{\varphi} &=& \mathbf{60^\circ} \\\\ r &=& \sqrt{ \left( \dfrac{1}{2} \right) ^2 + \left( \dfrac{\sqrt{3}}{2} \right) ^2 } \\ r &=& \sqrt{ \dfrac{1}{4} + \dfrac{3}{4} } \\ \mathbf{r} &=& \mathbf{1} \\ \hline \end{array} \)

\(\begin{array}{|rcll|} \hline && \mathbf{\left(\dfrac{1}{2} + \dfrac{\sqrt{3}}{2}i\right)^{2015}} \\ &=& \Big(\cos(60^\circ)+i\sin(60^\circ) \Big)^{2015} \\ &=& \cos(2015*60^\circ)+i\sin(2015*60^\circ) \\ &=& \cos(120900^\circ)+i\sin(120900^\circ) \\ &=& \cos(300^\circ)+i\sin(300^\circ) \\ &=& \mathbf{\dfrac{1}{2} - \dfrac{\sqrt{3}}{2}i} \\ \hline \end{array}\)

A no. when divided by 899 gives a remainder 63.
The remainder when this no. is divided by 29 is what?

\(\begin{array}{|rcll|} \hline x \equiv 63 \pmod{899} &\text{or}& x = 63+899n, n \in \mathbb{Z} \\\\ x \pmod{29} &\equiv& 63+899n \pmod{29} \quad | \quad 63 \pmod{29} = 5,\ 899n\pmod{29}= 0 \\ &\equiv& 5+0 \pmod{29} \\ &\equiv& 5 \pmod{29} \\ \hline \end{array} \)

The remainder when this no. is divided by 29 is \(\mathbf{5}\)

ABC is a right triangle with \(\angle B=90^\circ\), AB=5, BC=12, and AB tangent to a circle. 

CP and CQ are also tangent to the circle at P and Q. 

Find the length of chord \(\color{red}PQ\).

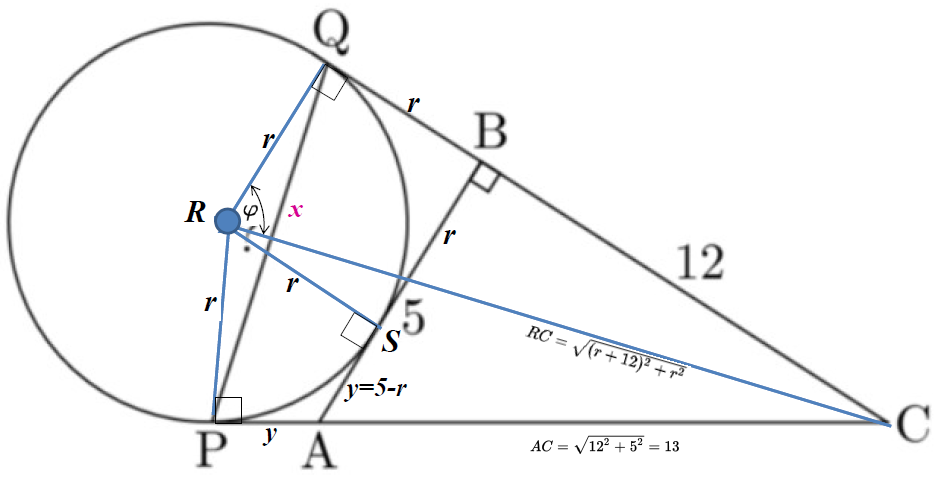
\(\text{Let $PQ=x$} \\ \text{Let $PC=QC$} \\ \text{Let $PA=AS=y$} \\ \text{Let $AC=\sqrt{12^2+5^2}=13$} \)

\(\begin{array}{|lrcll|} \hline (1): & PC &=& QC \quad | \quad QC = 12+r,\ PC=y+AC,\ AC= \sqrt{12^2+5^2}= 13 \\ & y+13 &=& 12+r \\ & \mathbf{y} &=& \mathbf{r-1} \\\\ (2): & AS &=& AB - SB \quad | \quad AS=y,\ AB=5,\ SB = r \\ & y &=& 5-r \\ & r &=& 5-y \quad | \quad y=r-1\\ & r &=& 5-(r-1) \\ & r &=& 5-r+1 \\ & 2r &=& 6 \\ & \mathbf{r} &=& \mathbf{3} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline RC &=& \sqrt{(r+12)^2+r^2 } \quad | \quad \mathbf{r=3} \\ RC &=& \sqrt{(3+12)^2+3^2 } \\ RC &=& \sqrt{15^2+3^2 } \\ \mathbf{RC} &=& \mathbf{\sqrt{234 }} \\ \hline \cos(\varphi) &=& \dfrac{RQ}{RC} \quad | \quad RQ=r=3,\ \mathbf{RC=\sqrt{234 }} \\ \cos(\varphi) &=& \dfrac{3}{\sqrt{234 }} \\ && \boxed{\text{Formula:} \cos(2\varphi)= 2\cos^2(\varphi)-1 } \\ \cos(2\varphi) &=& 2\cos^2(\varphi)-1 \quad | \quad \cos(\varphi) = \dfrac{3}{\sqrt{234 }}\\ \cos(2\varphi)&=& 2*\left(\dfrac{3}{\sqrt{234 }} \right)^2-1 \\ \cos(2\varphi)&=& 2*\dfrac{9}{ 234 }-1 \\ \cos(2\varphi)&=& \dfrac{9}{ 117 } -1 \\ \mathbf{\cos(2\varphi)} &=& \mathbf{-\dfrac{108}{ 117 }} \\ \hline \end{array} \)

cos-rule:

\(\begin{array}{|rcll|} \hline \mathbf{\text{In $\triangle RPQ$ }:} \\ \hline x^2 &=& r^2+r^2 -2rr\cos(2\varphi) \\ x^2 &=& 3^2+3^2 -2*3*3*\left(-\dfrac{108}{ 117 }\right) \\ x^2 &=& 18\left(1+\dfrac{108}{ 117 }\right) \\ x^2 &=& \dfrac{18*225}{ 117 } \\ x^2 &=& \dfrac{225}{ 6.5 } \\ \mathbf{x} &=& \mathbf{\dfrac{15}{ \sqrt{6.5} }} \\ \mathbf{x} &=&\mathbf{ 5.88348405415} \\ \hline \end{array}\)

The length of chord PQ is \(\mathbf{\approx 5.9}\)

AB is a line segment and M is its midpoint.
Semicircles are drawn with AB , AM and MB as diameters on the same side of line AB.
A circle with center O is drawn which touches the three semicircles,
then the radius of the smallest circle is equal to \(\dfrac{x}{y}*AB\).
Find \(\dfrac{x}{y}\).

\(\text{Let the radius of the smallest circle $=r$ }\\ \text{Let $R=\dfrac{AB}{4}$ }\)

\(\begin{array}{|rcll|} \hline (\mathbf{R+r)^2} &=& \mathbf{R^2+(2R-r)^2} \\ R^2+2Rr+r^2 &=& R^2+ 4R^2-4Rr+r^2 \\ 2Rr &=& 4R^2-4Rr \\ 2Rr+4Rr &=& 4R^2 \\ 6Rr &=& 4R^2 \quad | \quad :6R \\\\ r &=& \dfrac{4}{6}*R \\\\ r &=& \dfrac{2}{3}*R \quad | \quad R=\dfrac{AB}{4} \\\\ r &=& \dfrac{2}{3}*\dfrac{AB}{4} \\\\ r &=& \dfrac{1}{3}*\dfrac{AB}{2} \\\\ \mathbf{r} &=& \mathbf{\dfrac{1}{6}*AB} \\ \hline \end{array}\)

\(\mathbf{\dfrac{x}{y}=\dfrac{1}{6}} \)

Find the minimum value of the product \(P(x,y,z)=(2x+3y)(x+3z)(y+2z)\), when \(xyz=1\) and \(x\), \(y\), \(z\) are positive real numbers.

\(\mathbf{\huge{AM \geq GM }}\)

\(\begin{array}{|rcll|} \hline \dfrac{2x+3y}{2} & \ge & \sqrt{2x3y} \\\\ \dfrac{x+3z}{2} & \ge & \sqrt{x3z} \\\\ \dfrac{y+2z}{2} & \ge & \sqrt{y2z} \\\\ \hline \left( \dfrac{2x+3y}{2} \right) \left( \dfrac{x+3z}{2} \right) \left( \dfrac{y+2z}{2} \right) & \ge & \sqrt{6xy}\sqrt{3xz} \sqrt{2yz} \\\\ \dfrac{(2x+3y)(x+3z)(y+2z)}{8} & \ge & \sqrt{36x^2y^2z^2} \\\\ \dfrac{(2x+3y)(x+3z)(y+2z)}{8} & \ge & 6xyz \quad | \quad xyz=1 \\\\ \dfrac{(2x+3y)(x+3z)(y+2z)}{8} & \ge & 6*1 \\\\ \dfrac{(2x+3y)(x+3z)(y+2z)}{8} & \ge & 6 \\\\ (2x+3y)(x+3z)(y+2z) & \ge & 6 *8 \\\\ (2x+3y)(x+3z)(y+2z) & \ge & 48 \\\\ \mathbf{ 48 } & \le & \mathbf{(2x+3y)(x+3z)(y+2z)} \\ \hline \end{array}\)

The minimum value is \(\mathbf{ 48 }\)

ABC has a right angle at B. \(AC = 60\), \(AE = 52\) and \(CD=39\).
Find the length of \(DE\).

\(\text{Let $AD=t$ } \\ \text{Let $BD=w$ } \\ \text{Let $BE=u$ } \\ \text{Let $CE=v$ } \\ \text{Let $DE=\color{red}x$ }\)

\(\begin{array}{|lrcll|} \hline (1): & 60^2 &=& (u+v)^2+(t+w)^2 \\ (2): & 52^2 &=& u^2+(t+w)^2 \\ (3): & 39^2 &=& (u+v)^2+w^2 \\ (4): & x^2 &=& u^2+w^2 \\ \hline (4)+(1)-(2)-(3): \\ &x^2+60^2-52^2-39^2 &=& u^2+w^2 \\ &&& +(u+v)^2+(t+w)^2 \\ &&& - \left(u^2+(t+w)^2\right) \\ &&& -\left((u+v)^2+w^2 \right) \\\\ &x^2+60^2-52^2-39^2 &=& u^2+w^2 \\ &&& +(u+v)^2+(t+w)^2 \\ &&& - u^2-(t+w)^2 \\ &&& -(u+v)^2-w^2 \\\\ &x^2+60^2-52^2-39^2 &=& 0 \\ &x^2 &=& 52^2+39^2-60^2 \\ &x^2 &=& 625 \\ &\mathbf{x} &=& \mathbf{25} \\ \hline \end{array}\)

The length of DE is \(\mathbf{25}\)

Find all positive integers n such that n, n + 2, and n + 4 are all primes.

All prime numbers past 3 are of one of the form 6n+1 and 6n-1.

All integers are of one of this forms:
\(\begin{cases}6n-2 & \Rightarrow& 2·(3n-1) \\ \mathbf{6n -1} \\6n & \Rightarrow & 2·3·n \\ \mathbf{6n+1} \\ 6n+2 & \Rightarrow& 2·(3n+1) \\ 6n+3 & \Rightarrow & 3·(2n+1)\end{cases}\)

Note that all other than 6n-1 and 6n+1 can be expressed as a product of two integers bigger than 1.

So a prime number cannot be of any form other than \(\mathbf{6n\pm 1}\)

(That doesn't mean that all numbers of the form \(\mathbf{6n\pm 1}\) are prime)

So \(n=6n-1\), and \(n+2 = 6n+2\) , we see \(n+4 = 6n+3\) is always divisible by 3, so there is no more solution, if \(n > 3\).

The only solution is \(n=3\), \(n+2=5\), \(n+4= 7\)

If
\(x^2 + \dfrac{1}{x^2} = 171\),
then what are the possible values of
\(x - \dfrac{1}{x}\)?

\(\begin{array}{|rcll|} \hline \left(x - \dfrac{1}{x}\right)^2 &=& x^2-2*x*\dfrac{1}{x}+\dfrac{1}{x^2} \\\\ &=& x^2+\dfrac{1}{x^2}-\dfrac{2x}{x} \\\\ &=& x^2+\dfrac{1}{x^2}-2 \quad | \quad \mathbf{x^2 + \dfrac{1}{x^2} = 171} \\\\ &=& 171-2 \\\\ &=& \mathbf{169} \\ \hline x - \dfrac{1}{x} &=& \pm \sqrt{169} \\\\ \mathbf{x - \dfrac{1}{x}} &=& \mathbf{\pm 13} \\ \hline \end{array}\)

Compute

\(4 \cos(50^\circ) - \tan(40^\circ)\),

without using a calculator.  
 

How can I do this?

\(\begin{array}{|rcll|} \hline && \mathbf{4 \cos(50^\circ) - \tan(40^\circ)} \quad | \quad \cos(50^\circ)=\cos(90^\circ-40^\circ)=\sin(40^\circ) \\\\ &=& 4\sin(40^\circ) - \tan(40^\circ) \\\\ &=& 4 \sin(40^\circ)*\dfrac{\cos(40^\circ)}{\cos(40^\circ)} - \tan(40^\circ) \\\\ &=& \dfrac{2*2 \sin(40^\circ)\cos(40^\circ)} {\cos(40^\circ)} - \tan(40^\circ) \quad | \quad 2 \sin(40^\circ)\cos(40^\circ) = \sin(80^\circ) \\\\ &=& \dfrac{2\sin(80^\circ)} {\cos(40^\circ)} - \tan(40^\circ) \quad | \quad \sin(80^\circ)= \sin(180^\circ-80^\circ)=\sin(100^\circ) \\\\ &=& \dfrac{2\sin(100^\circ)} {\cos(40^\circ)} - \tan(40^\circ) \quad | \quad \cos(60^\circ)=\dfrac{1}{2} \ \text{or}\ 2=\dfrac{1}{\cos(60^\circ)} \\\\ &=& \dfrac{\sin(100^\circ)} {\cos(40^\circ)\cos(60^\circ)} - \tan(40^\circ) \\\\ &=& \dfrac{\sin(40^\circ+60^\circ)} {\cos(40^\circ)\cos(60^\circ)} - \tan(40^\circ) \\\\ &=& \dfrac{\sin(40^\circ)\cos(60^\circ)+\cos(40^\circ)\sin(60^\circ)} {\cos(40^\circ)\cos(60^\circ)} - \tan(40^\circ) \\\\ &=& \dfrac{\sin(40^\circ)\cos(60^\circ)} {\cos(40^\circ)\cos(60^\circ)}+ \dfrac{\cos(40^\circ)\sin(60^\circ)} {\cos(40^\circ)\cos(60^\circ)} - \tan(40^\circ) \\\\ &=& \dfrac{\sin(40^\circ)} {\cos(40^\circ)} + \dfrac{\sin(60^\circ)} {\cos(60^\circ)} - \tan(40^\circ) \\\\ &=& \tan(40^\circ) + \dfrac{\sin(60^\circ)} {\cos(60^\circ)} - \tan(40^\circ) \\\\ &=& \dfrac{\sin(60^\circ)} {\cos(60^\circ)} \quad | \quad \sin(60^\circ)=\dfrac{\sqrt{3}}{2},\ \cos(60^\circ)=\dfrac{1}{2} \\\\ &=& \dfrac{\sqrt{3}}{2} \above 1pt \dfrac{1}{2} \\\\ &=& \mathbf{\sqrt{3}} \\ \hline \end{array}\)

Let p and q be primes such that \(p + q = \left(p - q \right)^3\).  Find p and q.

\(\begin{array}{|rcll|} \hline p + q &=& \left(p - q \right)^3 \quad | \quad p = 5,\ q= 3\\ 5 + 3 &=& \left(5 - 3 \right)^3 \\ 8 &=& 2^3 \\ 8 &=& 8\ \checkmark \\ \hline \end{array}\)