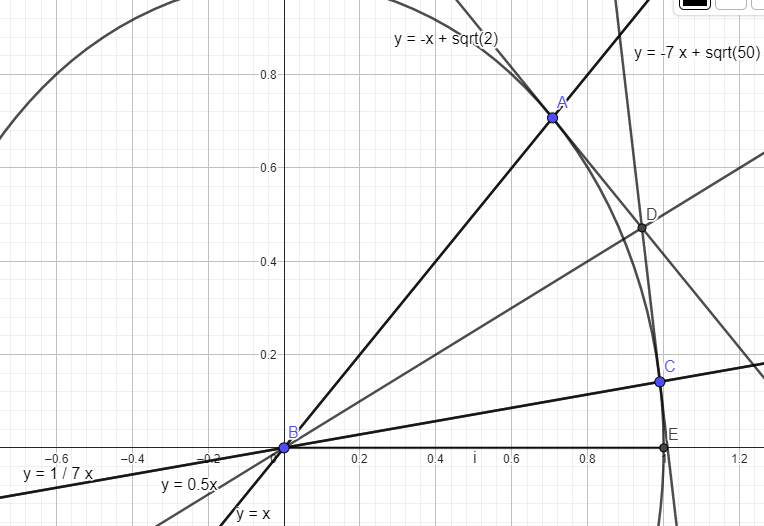
Another way
Construct a circle at the origin with a radius of 1
Equation is x^2 + y^2 = 1 (1)
Slope of line y = x = 1
So
x = y
Sub this into (1) for y
x^2 + x^2 = 1
2x^2 = 1
x^2 = 1/2
x= 1/sqrt 2 and y =1/sqrt 2
Construct a perpendicular line to y = x passing through (1/sqrt 2, 1/sqrt 2)
The equation is
y = (-1) (x - 1/sqrt 2) + 1/sqrt2 =
y = -x + 2/sqrt2
y = -x + sqrt 2 (2)
Now consider the line y = (1/7)x
Sub this into (1) for y
x^2 + (1/7 x )^2 =1
x^2 + 1/49 x^2 = 1
(50 /49) x^2 =1
x^2 = 49/50
x = 7 /sqrt (50)
y = (1/7) (7/sqrt (50) = 1 /sqrt (50)
Now construct a perpendicular line to y =(1/7)x passing through ( 7/sqrt 50 , 1/sqrt 50)
The equation is
y = (-7)(x - 7/sqrt50) + 1/sqrt (50)
y = -7x + 50/sqrt50
y = -7x + sqrt (50) ( 3)
Find the x intersection of (2) and (3)
-x + sqrt 2 = -7x + sqrt 50
6x = sqrt (50) - sqrt 2
6x = 5sqrt (2) - sqrt 2
6x = 4sqrt 2
x = (2/3)sqrt 2
And y = - (2/3)sqrt 2 + sqrt 2 = (1/3)sqrt 2
The intersection of these two lines is [ (2/3)sqrt 2 , (1/3)sqrt 2) ]
The slope of the line we want (through BD) = [ (1/3)sqrt 2 ] / [(2/3)sqrt 2 ] = 1/2 = .5 = m
(Which we found by calculator !!!)