heureka

find the derivative using implicit differentiation. \(\tan(x - y) = \dfrac{y}{5 + x^2}\)

Derivative: \((5 + x^2)\tan(x - y) -y=0\)

Formula: \(y'(x) = -\dfrac{F_x}{F_y}\)

\(\small{ \begin{array}{|rcll|} \hline \mathbf{F_x = \ ?} \\ \hline F_x &=& \dfrac{d }{dx}(5 + x^2)\tan(x - y)- \dfrac{d}{dx}y \quad | \quad \dfrac{d}{dx}y = 0 \\ F_x &=& \dfrac{d }{dx}(5 + x^2)\tan(x - y)-0 \\ F_x &=& \dfrac{d }{dx}(5 + x^2)\tan(x - y) \\ F_x &=& (5 + x^2)\dfrac{d }{dx}\tan(x - y)+\tan(x - y)\dfrac{d }{dx}(5 + x^2) \quad | \quad \dfrac{d }{dx}(5 + x^2) = 2x \\ F_x &=& (5 + x^2)\dfrac{d }{dx}\tan(x - y)+2x\tan(x - y)\dfrac{d }{dx} \quad | \quad \dfrac{d }{dx}\tan(x - y) = \dfrac{1}{\cos^2(x-y)}*1 \\ F_x &=& (5 + x^2)\dfrac{1}{\cos^2(x-y)}*1+2x\tan(x - y) \\ F_x &=& \dfrac{5 + x^2+2x\tan(x - y)\cos^2(x-y)}{\cos^2(x-y)} \\ F_x &=& \dfrac{5 + x^2+2x\sin(x - y)\cos(x-y)}{\cos^2(x-y)} \quad | \quad 2\sin(x - y)\cos(x-y) = \sin\Big(2(x-y)\Big) \\ \mathbf{F_x} &=& \mathbf{\dfrac{5 + x^2+x\sin\Big(2(x-y)\Big)}{\cos^2(x-y)}} \\ \hline \end{array} }\)

\(\small{ \begin{array}{|rcll|} \hline \mathbf{F_y = \ ?} \\ \hline F_y &=& \dfrac{d }{dy}(5 + x^2)\tan(x - y)- \dfrac{d}{dy}y \quad | \quad \dfrac{d}{dy}y = 1 \\ F_y &=& \dfrac{d }{dy}(5 + x^2)\tan(x - y)-1 \\ F_y &=& (5 + x^2)\dfrac{d }{dy}\tan(x - y)-1 \quad | \quad \dfrac{d }{dx}\tan(x - y) = \dfrac{1}{\cos^2(x-y)}*(-1) \\ F_y &=& (5 + x^2)\dfrac{1}{\cos^2(x-y)}*(-1) -1 \\ F_y &=& -\left( \dfrac{(5 + x^2)}{\cos^2(x-y)} +1 \right) \\ F_y &=& -\left( \dfrac{5 + x^2+\cos^2(x-y)}{\cos^2(x-y)} \right) \quad | \quad \cos^2(x-y)=\dfrac{1+ \cos\Big(2(x-y)\Big)}{2} \\ F_y &=& -\left( \dfrac{5 + x^2+\dfrac{1+ \cos\Big(2(x-y)\Big)}{2}}{\cos^2(x-y)} \right) \\ F_y &=& -\left( \dfrac{10 + 2x^2+1+ \cos\Big(2(x-y)\Big)}{2\cos^2(x-y)} \right) \\ \mathbf{F_y} &=& \mathbf{ -\left( \dfrac{11 + 2x^2+\cos\Big(2(x-y)\Big)}{2\cos^2(x-y)} \right)} \\ \hline \end{array} }\)

\(\begin{array}{|rcll|} \hline y'(x) &=& -\dfrac{F_x}{F_y} \\\\ y'(x) &=& -\dfrac{\dfrac{5 + x^2+x\sin\Big(2(x-y)\Big)}{\cos^2(x-y)}} {-\left( \dfrac{11 + 2x^2+\cos\Big(2(x-y)\Big)}{2\cos^2(x-y)} \right)} \\\\ y'(x) &=& \dfrac{\dfrac{5 + x^2+x\sin\Big(2(x-y)\Big)}{\cos^2(x-y)}} {\dfrac{11 + 2x^2+\cos\Big(2(x-y)\Big)}{2\cos^2(x-y)} } \\\\ y'(x) &=& \dfrac{ 2\left( 5 + x^2+ x\sin \Big(2(x-y)\Big) \right) } { 11 + 2x^2 +\cos\Big(2(x-y)\Big)} \\\\ \mathbf{y'(x)} &=& \mathbf{\dfrac{ 2\Big( 5 + x^2+ x\sin(2x-2y) \Big) } { 11 + 2x^2 +\cos(2x-2y)} } \\ \hline \end{array}\)

You have linear functions \(p(x)\) and \(q(x)\). You know \(p(2)=3\), and \(p(q(x))=4x+7\) for all \(x\).

Find \(q(-1)\).

\(\begin{array}{|l|} \hline p(q(x)) = 4x+7,\\ \text{if $q(x) = 2$, then $4x+7 = 3$, so $4x= 3-7$ or $4x = -4$ hence $\mathbf{x=-1}$ } \\ \mathbf{q(-1)=2} \\ \hline \end{array}\)

What is the distance between the two intersections of \(y=x^2\) and \(x+y=1\)?

\(\begin{array}{|lrcll|} \hline & \text{intersections:} \\ \hline (1) & y &=& x^2 \\ \\ (2) & x+y &=& 1 \quad | \quad y = x^2 \\ & x+x^2 &=& 1 \\ & \mathbf{x^2+x-1} &=& \mathbf{0} \\ & x &=& \frac{-1\pm \sqrt{1-4(-1)} }{2} \\ & x &=& \frac{-1\pm\sqrt{5} }{2} \\ & \mathbf{x_1 = \dfrac{-1+\sqrt{5} }{2}} && \mathbf{x_2 = \dfrac{-1-\sqrt{5} }{2}} \\ \hline \end{array} \)

\(\begin{array}{|rcl|rcl|} \hline x_1-x_2 &=& \dfrac{-1+\sqrt{5} }{2}-\dfrac{-1-\sqrt{5} }{2} & x_1+x_2 &=& \dfrac{-1+\sqrt{5} }{2}+\dfrac{-1-\sqrt{5} }{2} \\\\ &=& -\frac{1}{2} +\frac{\sqrt{5} }{2}+\frac{1}{2}+\frac{\sqrt{5} }{2} & &=& -\frac{1}{2} +\frac{\sqrt{5} }{2}-\frac{1}{2}-\frac{\sqrt{5} }{2} \\\\ \mathbf{x_1-x_2} &=& \mathbf{\sqrt{5}} &\mathbf{x_1+x_2} &=& \mathbf{-1} \\ \mathbf{\left(x_1-x_2\right)^2} &=& \mathbf{5} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline y_1-y_2 &=& x_1^2-x_2^2 \\ &=& (x_1 -x_2)(x_1 +x_2) \\ &=& \sqrt{5}(-1) \\ \mathbf{y_1-y_2} &=& \mathbf{-\sqrt{5}} \\ \mathbf{\left(y_1-y_2\right)^2} &=& \mathbf{5} \\ \hline \end{array} \)

\(\begin{array}{|rcll|} \hline \text{The distance} \\ \hline &=& \sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2} \\ &=& \sqrt{5+5} \\ &=& \sqrt{10} \\ &=&\mathbf{ 3.16227766017\ldots} \\ \hline \end{array}\)

vectors

\(\begin{array}{|rcll|} \hline p\cdot u &=& ||p|| * ||u|| * \cos(\alpha) \quad | \quad \cos(\alpha)= \dfrac{6}{11} \\\\ p\cdot u &=& 6 * 11 * \dfrac{6}{11} \\ \mathbf{p\cdot u} &=& \mathbf{36} \\ \hline \end{array}\)

point H is located at (-7,5) where is h after a 270 degree clockwise rotation

Let \(270^\circ\) clockwise rotation = \(90^\circ\) counter clockwise  rotation

\(\begin{array}{|lrcll|} \hline & && \text{complex} \\ \hline (-7,\ 5) \rightarrow & && ( -7+5i) \\ & && ( -7+5i)\times i & \times i ~(\text{ $90^\circ$ counter clockwise rotation}) \\ & &=&-7i+5i\times i \\ & &=&-7i+5i^2 \quad i^2 = -1 \\ & &=&-7i-5\\ (-5,\ -7) \leftarrow & &=&(-5-7i)\\ \hline \end{array} \)

Let \(\mathbf{a}\) be a vector of length 2, and let \(\mathbf{b}\) and \(\mathbf{c} \) be vectors such that
\(\mathbf{a} \bullet \mathbf{b} = 3,\ \mathbf{a} \bullet \mathbf{c} = 4,\ \mathbf{b} \bullet \mathbf{c} = 5\).
Find \(\mathbf{a}\bullet( \mathbf{b} + \mathbf{c}),\ \mathbf{b}\bullet(\mathbf{a} +\mathbf{b} + \mathbf{c}),\ (\mathbf{a} + 2\mathbf{b})\bullet(-3\mathbf{a} + 3\mathbf{c})\).
If any of these cannot be uniquely determined from the information given, enter a question mark.

\(\mathbf{a}\bullet( \mathbf{b} + \mathbf{c})\\ \begin{array}{|rcll|} \hline && \mathbf{a}\bullet( \mathbf{b} + \mathbf{c}) \\ &=& \mathbf{a}\bullet\mathbf{b}+\mathbf{a}\bullet \mathbf{c} \quad | \quad \mathbf{a} \bullet \mathbf{b} = 3,\ \mathbf{a} \bullet \mathbf{c} = 4 \\ &=& 3+4 \\ &=& \mathbf{7} \\ \hline \end{array} \)

\(\mathbf{b}\bullet(\mathbf{a} +\mathbf{b} + \mathbf{c}) \\ \begin{array}{|rcll|} \hline && \mathbf{b}\bullet(\mathbf{a} +\mathbf{b} + \mathbf{c}) \\ &=& \mathbf{b}\bullet \mathbf{a} + \mathbf{b}\bullet\mathbf{b} + \mathbf{b}\bullet\mathbf{c} \\ &=& \mathbf{a}\bullet \mathbf{b} + \mathbf{b}\bullet\mathbf{b} + \mathbf{b}\bullet\mathbf{c} \\ &=& 3 + \mathbf{b}\bullet\mathbf{b} + 5 \\ &=& 8 + \mathbf{b}\bullet\mathbf{b} \\ &=& ? \\ \hline \end{array} \)

\((\mathbf{a} + 2\mathbf{b})\bullet(-3\mathbf{a} + 3\mathbf{c}) \\ \begin{array}{|rcll|} \hline && (\mathbf{a} + 2\mathbf{b})\bullet(-3\mathbf{a} + 3\mathbf{c}) \\ &=& (-3)\mathbf{a}\bullet\mathbf{a}+3\mathbf{a}\bullet\mathbf{c}-6\mathbf{b}\bullet\mathbf{a}+6\mathbf{b}\bullet\mathbf{c} \\ &=& (-3)\mathbf{a}\bullet\mathbf{a}+3\mathbf{a}\bullet\mathbf{c}-6\mathbf{a}\bullet\mathbf{b}+6\mathbf{b}\bullet\mathbf{c} \quad | \quad \mathbf{a}\bullet\mathbf{a} = 2^2 \\ &=& (-3)*2^2+3*4-6*3+6*5 \\ &=& -12+12-18+30 \\ &=& -18+30 \\ &=& \mathbf{12} \\ \hline \end{array} \)

Hi Melody,

many thanks for the detailed answer!

Let \(a\) and \(b\) be the roots of \(y^2 + 5y - 11 = 0\).
Find \((a + 3)(b + 3)\).

Vieta's formulas:  \(\begin{array}{|rcll|} \hline y^2 \underbrace{+5}_{=-(a+b)}y \underbrace{- 11}_{=ab} &=& 0 \\ \hline \end{array} \)

\(\begin{array}{|rcll|} \hline ab&=& -11 \\ a+b &=& -5 \\\\ && \mathbf{(a+3)(b+3)} \\ &=& ab+3a+3b+9 \\ &=& ab+3(a+b) +9 \\ &=& -11+3(-5) + 9 \\ &=& -11-15+9 \\ &=& \mathbf{-17} \\ \hline \end{array}\)

The vertices of a convex pentagon are (-1,-1), (-3,4), (1,7), (6,5), and (3,-1).
What is the area of the pentagon .

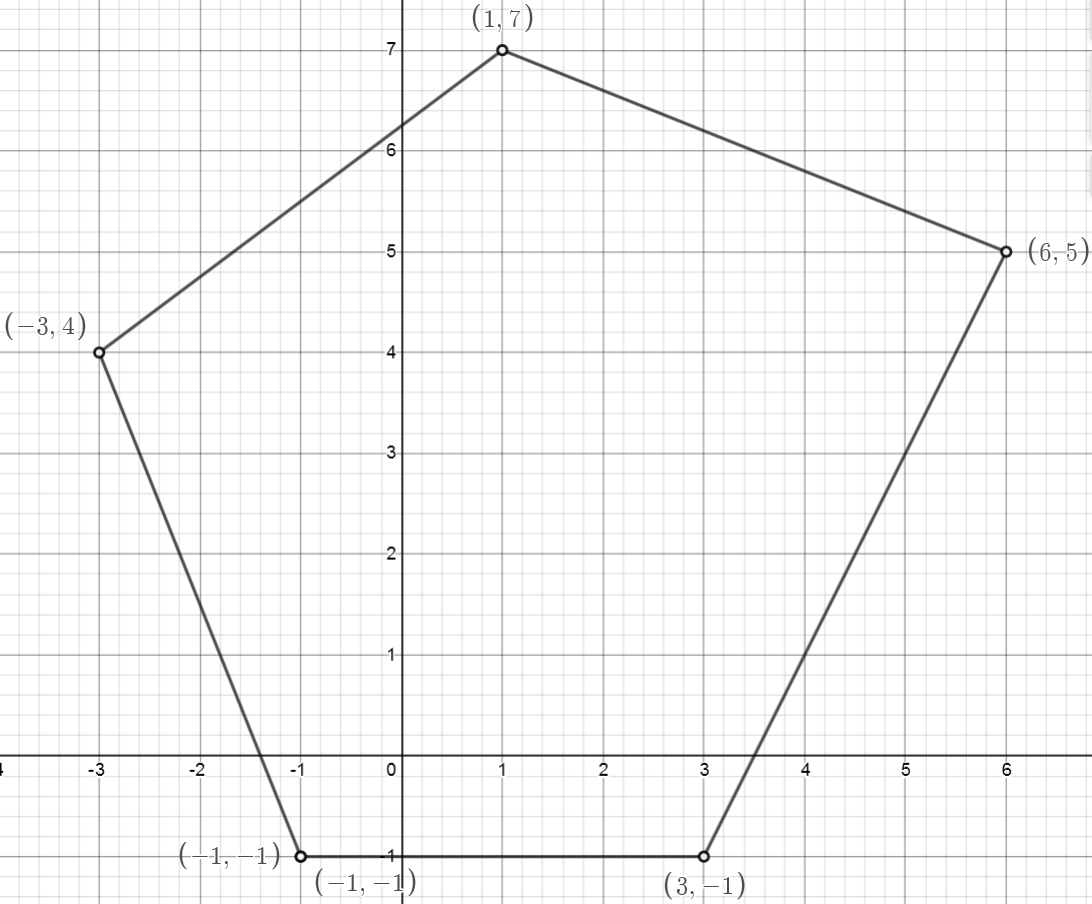
Use the Gauss's shoelace area formula. Fill the table in counterclockwise.

\(\begin{array}{|lll|} \hline \mathbf{\text{The area of a convex pentagon } }: \\ \begin{array}{r|rr|c} \hline \text{Point} & x & y & \text{cross products} \\ \hline (-1,~-1): & -1 & -1 \\ & & & (-1)*(-1) -(3)*(-1) \\ (3,~-1): & 3 & -1 \\ & & & 3*5 -6*(-1) \\ (6,~5): & 6 & 5 & \\ & & & 6*7-1*5 \\ (1,~7): & 1 & 7 & \\ & & & 1*4 -(-3)*7 \\ (-3,~4): & -3 & 4 & \\ & & & (-3)*(-1) -(-1)*4 \\ (-1,~-1): & -1 & -1 & \\ \hline & & & \text{sum }~=1+3+15+6+42-5+4+21+3+4 \\ & & & \mathbf{=94} \\ \hline \end{array}\\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \text{The area of the convex pentagon} &=& \dfrac{1}{2}*\text{sum} \\\\ &=& \dfrac{94}{2} \\\\ &=& \mathbf{47} \\ \hline \end{array}\)