heureka

H is the orthocenter of acute triangle ABC and the extensions of AH, BH, and CH intersect the circumcircle
of triangle ABC at A', B' and C'.
We know angle AHB:angle BHC:angle CHA=9:10:11.
Find angle A'B'C' in degrees.

\(\begin{array}{|rcll|} \hline \mathbf{\angle AHB:\angle BHC:\angle CHA} &=& \mathbf{9:10:11} \\\\ \frac{\angle AHB}{\angle CHA} &=& \frac{9}{11} \\ \angle AHB &=& \frac{9}{11} *( \angle CHA ) \\\\ \frac{\angle BHC}{\angle CHA} &=& \frac{10}{11} \\ \angle BHC &=& \frac{10}{11}*(\angle CHA ) \\\\ \angle AHB+\angle BHC+\angle CHA &=& 360^\circ \\ \frac {9}{11} *( \angle CHA )+\frac{10}{11}*(\angle CHA )+\angle CHA &=& 360^\circ \\ \frac {19}{11} *( \angle CHA )+\angle CHA &=& 360^\circ \\ \frac {30}{11} *( \angle CHA ) &=& 360^\circ \\ \angle CHA &=& \frac {11}{30} *360^\circ \\ \mathbf{\angle CHA} &=& \mathbf{132^\circ} \\ \hline \end{array}\)

\(\text{$\angle A'B'C'$ in degrees is $2*42^\circ = 84^\circ$}\)

Consider the series. 

\(\sum \limits_{n=1}^{\infty} \dfrac{1+4n} {4^{n+1}}\)

\(\begin{array}{|rcll|} \hline \mathbf{\sum \limits_{n=1}^{\infty} \dfrac{1+4n} {4^{n+1}}} &=& \sum \limits_{n=1}^{\infty} \dfrac{1+4n} {4^{n}*4} \\\\ &=& \dfrac{1}{4} \left( \sum \limits_{n=1}^{\infty} \dfrac{1+4n} {4^{n}} \right) \\\\ &=& \dfrac{1}{4} \left[ \sum \limits_{n=1}^{\infty} (1+4n) \left( \dfrac{1}{4}\right)^{n} \right] \\\\ &=& \dfrac{1}{4} \left[ -1 + \sum \limits_{n=1}^{\infty} \Big(1+4(n-1)\Big) \left( \dfrac{1}{4}\right)^{n-1} \right] \\\\ \mathbf{\sum \limits_{n=1}^{\infty} \dfrac{1+4n} {4^{n+1}}} &=& \mathbf{\dfrac{1}{4}( -1 + s )} \qquad \boxed{s=\sum \limits_{n=1}^{\infty} \Big(1+4(n-1)\Big) \left( \dfrac{1}{4}\right)^{n-1} } \\ \hline \end{array}\)

Infinite arithmetico-geometric sequence:

\(\begin{array}{|rcll|} \hline s &=& \sum \limits_{n=1}^{\infty} \Big(1+4(n-1)\Big) \left( \dfrac{1}{4}\right)^{n-1} \\ \hline \end{array}\)

\({\color{red}a}{\color{blue}b }+(a+d){\color{blue}br }+{\color{red}(a+2d)}{\color{blue}br^2 }+{\color{red}(a+3d)}{\color{blue}br^3 }+\cdots + {\color{red}\Big(a+(n-1)d \Big)}{\color{blue}br^{n-1} } + \cdots\)

\(\begin{array}{|lrcll|} \hline \text{arithmetical sequence:}\quad 1+5+9+13+17+\ldots \\ {\color{red}1}+({\color{red}1}+1*{\color{orange}4})+({\color{red}1}+2*{\color{orange}4})+({\color{red}1}+3*{\color{orange}4})+\dotsb+\Big({\color{red}1}+(n-1)*{\color{orange}4}\Big)+\dotsb \\ \boxed{a={\color{red}1},\ d={\color{orange}4} \text{ is the common difference} } \\\\ \text{geometric series:}\quad 1+1*\frac{1}{4^1}+1*\frac{1}{4^2}+ 1*\frac{1}{4^3}+ 1*\frac{1}{4^4}+\cdots \\ {\color{blue}1} +{\color{blue}1}*\left({\color{green}\frac{1}{4}}\right)^1 +{\color{blue}1}*\left({\color{green}\frac{1}{4}}\right)^2 +{\color{blue}1}*\left({\color{green}\frac{1}{4}}\right)^3 +\dotsb +{\color{blue}1}*\left({\color{green}\frac{1}{4}}\right)^{n-1} +\dotsb\\ \boxed{ b={\color{blue}1},\ r={\color{green}\frac{1}{4}}\ \text{ is the common ratio} } \\ \hline \end{array} \)

Formula:
sum of a infinite arithmetico-geometric sequence: \(\begin{array}{|rcll|} \hline \mathbf{s} &=& \mathbf{\left(\dfrac{b}{1-r}\right) \Bigg( a+d\left( \dfrac{r}{1-r} \right) \Bigg)} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{s} &=& \mathbf{\left(\dfrac{b}{1-r}\right) \Bigg( a+d\left( \dfrac{r}{1-r} \right) \Bigg)} \\\\ && \boxed{a={\color{red}1},\ d={\color{orange}4} \text{ is the common difference} } \\ &&\boxed{ b={\color{blue}1 },\ r={\color{green}\frac{1}{4}}\ \text{ is the common ratio} } \\\\ s &=& \left(\dfrac{{\color{blue}1} }{1-{ \color{green}\frac{1}{4}} }\right) \Bigg( {\color{red}1} + { \color{orange}4} \left( \dfrac{ {\color{green}\frac{1}{4} }}{1-{\color{green}\frac{1}{4}} } \right) \Bigg) \\\\ s &=& \dfrac{4}{3}\left( {\color{red}1} + \dfrac{4}{3} \right) \\\\ s &=& \dfrac{4}{3} *\dfrac{7}{3} \\\\ \mathbf{s} &=& \mathbf{\dfrac{28}{9}} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{\sum \limits_{n=1}^{\infty} \dfrac{1+4n} {4^{n+1}}} &=& \mathbf{\dfrac{1}{4}( -1 + s )} \quad | \quad s=\dfrac{28}{9} \\\\ &=& \dfrac{1}{4}\left( -1 + \dfrac{28}{9} \right) \\\\ &=& \dfrac{1}{4}\left( \dfrac{19}{9} \right) \\\\ \mathbf{\sum \limits_{n=1}^{\infty} \dfrac{1+4n} {4^{n+1}}} &=& \mathbf{\dfrac{19}{36}} \\ \hline \end{array}\)

Compute the distance between the parallel lines given by  \(\begin{pmatrix} 1 \\ 4 \end{pmatrix} + t \begin{pmatrix} 4 \\ 3 \end{pmatrix}\)
and \(\begin{pmatrix} -5 \\ 6 \end{pmatrix} + s \begin{pmatrix} 4 \\ 3 \end{pmatrix}\).

\(\text{The orthogonal vector of the lines and normalized is }\\ \binom{-3}{4}*\frac{1}{\sqrt{(-3)^2+4^2}}~\text{ or }~\binom{4}{-3}*\frac{1}{\sqrt{3^2+(-4)^2}} \\ \text{because } \binom{4}{3}\binom{-3}{4} = 0 ~\text{ respectively }~\binom{4}{3}\binom{4}{-3} = 0\\ \)

\(\text{Let $ \hat{n} = \frac{1}{5}\binom{-3}{4}$} \)

The distance between the parallel lines is:

\(\begin{array}{|rcll|} \hline d &=&\dfrac{1}{5}\dbinom{-3}{4}\dbinom{-5}{6}-\frac{1}{5}\dbinom{-3}{4}\dbinom{1}{4} \\\\ d &=&\dfrac{1}{5}\Big(15+24-( -3+16 ) \Big) \\\\ d &=&\dfrac{26}{5} \\\\ \mathbf{d} &=& \mathbf{5.2} \\ \hline \end{array}\)

Let
\(\mathbf{v} \text{ and } \mathbf{w} \text{ be vectors such that } \operatorname{proj}_{\mathbf{w}}( \mathbf{v} )= \begin{pmatrix} 4 \\ -7 \end{pmatrix}\).
Find
\(\operatorname{proj}_{-2 {\mathbf{w}}} (3 {\mathbf{v}})\).

\(\begin{array}{|rcll|} \hline \vec{p} &=& \operatorname{proj}_{\mathbf{w}}( \mathbf{v} ) \\\\ &=& \dbinom{4}{-7} \\\\ &=& \dfrac{\vec{w}\vec{v}}{w^2}\vec{w} \\ \hline \vec{P} &=& \operatorname{proj}_{\mathbf{-2w}}( \mathbf{3v} ) \\\\ &=& \dfrac{(-2\vec{w})(3\vec{v})}{|-2w|^2}(-2\vec{w}) \\\\ &=& 6\dfrac{\vec{w}\vec{v}}{2w^2}\vec{w} \\\\ &=& 3\dfrac{\vec{w}\vec{v}}{w^2}\vec{w} \\\\ &=& 3\vec{p} \\\\ &=& 3\dbinom{4}{-7} \\\\ &=& \dbinom{12}{-21} \\ \hline \end{array}\)

\(\operatorname{proj}_{-2 {\mathbf{w}}} (3 {\mathbf{v}}) = \dbinom{12}{-21}.\)

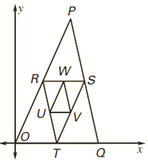
In the diagram, O is lacated at (0,0), U is located at (7,6),
and V is located at (11,6).
Assume that R, S, T, U, V, and W are midpoints.

\(1)\\ \begin{array}{|rcl|rcl|rcl|} \hline R &=& U + \dfrac{TR}{2} & \dfrac{TR}{2}+T &=& U & T &=& \dfrac{Q}{2} \\ && & \dfrac{TR}{2}+\dfrac{Q}{2} &=& U \\ && & \dfrac{TR}{2} &=& U-\dfrac{Q}{2} \\ R &=& U + U-\dfrac{Q}{2} \\ \mathbf{R} &=& \mathbf{2U-\dfrac{Q}{2}} \\ \hline S &=& T+TS & T+\dfrac{TS}{2} &=& V & T &=& \dfrac{Q}{2} \\ & & & \dfrac{Q}{2}+\dfrac{TS}{2} &=& V \quad | \quad *2 \\ & & & Q+TS &=& 2V \\ & & & TS &=& 2V-Q \\ S &=& \dfrac{Q}{2} + 2V-Q \\ \mathbf{S} &=& \mathbf{2V-\dfrac{Q}{2}} \\ \hline \end{array}\)

\(2)\\ \begin{array}{|rcl|rcl|rcl|} \hline && &P &=& S + \dfrac{QP}{2} & QP &=& 2(S-Q) \\ && &P &=& S + (S-Q) \\ && &P &=& 2S-Q & S&=&2V-\dfrac{Q}{2} \\ && &P &=& 4V-Q-Q \\ && &\mathbf{P} &=& \mathbf{4V-2Q} \\ \hline && &P &=& 2R & R&=&2U-\dfrac{Q}{2} \\ && &\mathbf{P} &=& \mathbf{4U-Q} \\ P= 4U-Q &=& 4V-2Q \\ 4U-Q &=& 4V-2Q \\ \mathbf{ Q }&=& \mathbf{4V-4U} \\ \hline \end{array} \\ 3)\\ \begin{array}{|rcl|rcl|rcl|} \hline W&=& \dfrac{1}{2}( R+S )& R&=&2U-\dfrac{Q}{2} & S&=&2V-\dfrac{Q}{2} \\ W&=& \dfrac{1}{2}( 2U-\dfrac{Q}{2}+2V-\dfrac{Q}{2} ) \\ W&=& \dfrac{1}{2}( 2U+2V-Q ) \\ \mathbf{ W }&=& \mathbf{U+V-\dfrac{Q}{2}} \\ \hline \end{array}\)

\(\text{Summary:}\quad Q=4V-4U \\ \begin{array}{|rcll|} \hline T&=& \dfrac{Q}{2} \\ R&=& 2U-\dfrac{Q}{2} \\ S&=& 2V-\dfrac{Q}{2} \\ W&=& U+V-\dfrac{Q}{2} \\ P&=& 4U-Q \\ \hline \end{array}\)

Substitute \(Q\):

\(\begin{array}{|rcll|} \hline T &=& -2U+2V \\ Q &=& -4U+4V \\ R &=& 4U-2V \\ S &=& 2U \\ W &=& 3U-V \\ P &=& 8U-4V \\ \hline \end{array}\)

Substitute \(U(7,6)\) and \(V(11,6)\):

\(\begin{array}{|rcll|} \hline \mathbf{T} &=& -2(7,6)+2(11,6) = (-14+22, -12+12) =\mathbf{(8,0)}\\ \mathbf{Q} &=& -4(7,6)+4(11,6) = (-28+44, -24+24) =\mathbf{(16,0)}\\ \mathbf{R} &=& 4(7,6)-2(11,6) = (28-22, 24-12) =\mathbf{(6,12)}\\ \mathbf{S} &=& 2(7,6) = \mathbf{(14, 12)} \\ \mathbf{W} &=& 3(7,6)-(11,6) = (21-11, 18-6) =\mathbf{(10,12)}\\ \mathbf{P} &=& 8(7,6)-4(11,6) = (56-44, 48-24) =\mathbf{(12,24)}\\ \hline \end{array}\)

On Monday, Jessica told two friends a secret. On Tuesday, each of those friends told the secret to two other friends. Each time a student heard the secret, he or she told the secret to two other friends the following day. On what day of the week will 1023 students know the secret?

\(\begin{array}{|r|r|l|} \hline \text{day of the week} & & \text{sum} \\ \hline \text{Jessica} & 1 = 2^0 & 1\\ \text{Monday} & 2 = 2^1 & 2^2-1 = 3 \\ \text{Tuesday} & 2*2 = 2^2 & 2^3-1 = 7 \\ \text{Wednesday}& = 2^3 & 2^4-1 = 15 \\ \text{Thursday} & = 2^4 & 2^5-1 = 31 \\ \text{Friday} & = 2^5 & 2^6-1 = 63 \\ \text{Saturday} & = 2^6 & 2^7-1 = 127 \\ \text{Sunday} & = 2^7 & 2^8-1 = 255 \\ \text{Monday} & = 2^8 & 2^9-1 = 511 \\ \color{red}\text{Tuesday} & = 2^9 & 2^{10}-1 = 1023 \\ \hline \end{array} \)

Find all \(n\)  for which \(n!+(n+1)!+(n+2)!\) is a perfect square.

\(\begin{array}{|rcll|} \hline && n!+(n+1)!+(n+2)! \\ &=& n! + n!(n+1)+n!(n+1)(n+2) \\ &=& n!\Big(1+(n+1)+(n+1)(n+2)\Big) \\ &=& n!\Big(n^2+4n+4\Big) \\ &=& \mathbf{n!(n+2)^2} \\ \hline \end{array} \)

\(n!+(n+1)!+(n+2)!\) is a perfect square, if \(n!\) is a perfect square!

But n! is only a perfect square, if \(n=0 ~(0!=1=1^2)\) or \(n = 1~ (1!=1=1^2)\)

\(\begin{array}{|lrcll|} \hline n=0: & 0!+1!+2! = 1+1+2 = 4 = 2^2 \\ n=1: & 1!+2!+3! =1+2+6 = 9 = 3^2 \\ \hline \end{array}\)

A series is given by
\(\dfrac{1}{7^1}+\dfrac{2}{7^2}+\dfrac{3}{7^3}+\dfrac{4}{7^4}+\dfrac{5}{7^5}+\cdots \).

This is a infinite arithmetico-geometric sequence.

In general: \({\color{red}a}{\color{blue}b }+(a+d){\color{blue}br }+{\color{red}(a+2d)}{\color{blue}br^2 }+{\color{red}(a+3d)}{\color{blue}br^3 }+\cdots + {\color{red}\Big(a+(n-1)d \Big)}{\color{blue}br^{n-1} } + \cdots \)

\(\begin{array}{|lrcll|} \hline \text{arithmetical sequence:}\quad 1+2+3+4+5+\ldots \\ {\color{red}1}+({\color{red}1}+1*{\color{orange}1})+({\color{red}1}+2*{\color{orange}1})+({\color{red}1}+3*{\color{orange}1})+\dotsb+\Big({\color{red}1}+(n-1)*{\color{orange}1}\Big)+\dotsb \\ \boxed{a={\color{red}1},\ d={\color{orange}1} \text{ is the common difference} } \\\\ \text{geometric series:}\quad \frac{1}{7^1}+\frac{1}{7^2}+ \frac{1}{7^3}+ \frac{1}{7^4}+ \frac{1}{7^5}+\cdots \\ {\color{blue}\frac{1}{7} } +{\color{blue}\frac{1}{7} }\left({\color{green}\frac{1}{7}}\right)^1 +{\color{blue}\frac{1}{7} }\left({\color{green}\frac{1}{7}}\right)^2 +{\color{blue}\frac{1}{7} }\left({\color{green}\frac{1}{7}}\right)^3 +\dotsb +{\color{blue}\frac{1}{7} }\left({\color{green}\frac{1}{7}}\right)^{n-1} +\dotsb\\ \boxed{ b={\color{blue}\frac{1}{7} },\ r={\color{green}\frac{1}{7}}\ \text{ is the common ratio} } \\ \hline \end{array} \)

Formula:
sum of a infinite arithmetico-geometric sequence

\(\begin{array}{|rcll|} \hline \mathbf{s} &=& \mathbf{\left(\dfrac{b}{1-r}\right) \Bigg( a+d\left( \dfrac{r}{1-r} \right) \Bigg)} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{s} &=& \mathbf{\left(\dfrac{b}{1-r}\right) \Bigg( a+d\left( \dfrac{r}{1-r} \right) \Bigg)} \\\\ && \boxed{a={\color{red}1},\ d={\color{orange}1} \text{ is the common difference} } \\ &&\boxed{ b={\color{blue}\frac{1}{7} },\ r={\color{green}\frac{1}{7}}\ \text{ is the common ratio} } \\\\ s &=& \left(\dfrac{{\color{blue}\frac{1}{7}} }{1-{ \color{green}\frac{1}{7}} }\right) \Bigg( {\color{red}1} + { \color{orange}1} \left( \dfrac{ {\color{green}\frac{1}{7} }}{1-{\color{green}\frac{1}{7}} } \right) \Bigg) \\\\ s &=& \frac{1}{7}*\frac{7}{6} \left( {\color{red}1} + \frac{1}{7}*\frac{7}{6} \right) \\\\ s &=& \frac{1}{6} \left( {\color{red}1} + \frac{1}{6} \right) \\\\ s &=& \frac{1}{6} *\frac{7}{6} \\\\ \mathbf{s} &=& \mathbf{\frac{7}{36}} \\ \hline \end{array}\)

\(\mathbf{\dfrac{1}{7^1}+\dfrac{2}{7^2}+\dfrac{3}{7^3}+\dfrac{4}{7^4}+\dfrac{5}{7^5}+\cdots} = \mathbf{\dfrac{7}{36}}\)

How many numbers are in the list \(3\dfrac23,\, 4\dfrac13,\, 5,\, 5\dfrac23,\, \ldots,\, 26\dfrac13,\, 27\) ?

\(\begin{array}{|rcll|} \hline && 3\dfrac23,\, 4\dfrac13,\, 5,\, 5\dfrac23,\, \ldots,\, 26\dfrac13,\, 27 \\\\ &=& \dfrac{11}3,\, \dfrac{13}3,\, \dfrac{15}3,\, \dfrac{17}3,\, \ldots,\, \dfrac{79}3,\, \dfrac{81}3 \\\\ \text{arithmetic progression, formula: }\quad \mathbf{a_n} &=& \mathbf{a_1+(n-1)d} \\\\ && a_1 = \dfrac{11}3,\qquad a_n = \dfrac{81}3,\qquad d = \dfrac{2}3 \\\\ \dfrac{81}3 &=& \dfrac{11}3+(n-1)\dfrac{2}3 \\\\ \dfrac{81}3- \dfrac{11}3 &=& (n-1)\dfrac{2}3 \\\\ \dfrac{70}3 &=& (n-1)\dfrac{2}3 \quad | \quad *3 \\\\ 70 &=& (n-1)*2 \quad | \quad :2 \\\\ 35 &=& n-1 \\\\ n &=& 35+1 \\\\ \mathbf{n} &=& \mathbf{36} \\ \hline \end{array}\)

Thank you, CPhill !