heureka

In a box there are 9 balls, 5 of them are white balls and 4 others are red balls so i decided to take 3 balls from the box.
What is the probabilty i get at least 1 red ball?

In a box there are 9 balls, 5 of them are white balls and 4 others are red balls so i decided to take 3 balls from the box.

What is the probabilty i get at least 1 red ball?

\(\begin{array}{|rcll|} \hline && 1-\dfrac{5}{9}*\dfrac{4}{8}*\dfrac{3}{7} \\\\ &=& 1-\dfrac{60}{504} \\\\ &=& \mathbf{\dfrac{444}{504}} \\ \hline \end{array} \)

Find AC.

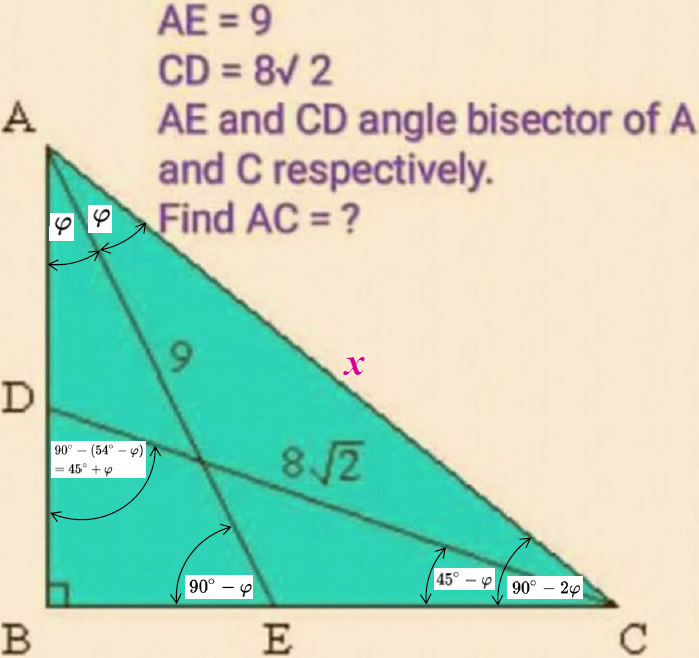
\(\text{Let $AB=c$ }\\ \text{Let $BC=a$ }\\ \text{Let $AC=x$ }\)

\(\begin{array}{|rcll|} \hline \mathbf{\text{In }\triangle ABE:} \\ \hline \sin(90^\circ-\varphi) &=& \dfrac{c}{9} \\\\ \cos(\varphi) &=& \dfrac{c}{9} \\\\ \mathbf{c} &=&\mathbf{ 9\cos(\varphi)} \qquad (1) \\ \hline \end{array} \begin{array}{|rcll|} \hline \mathbf{\text{In }\triangle ABC:} \\ \hline \sin(90^\circ-2\varphi) &=& \dfrac{c}{x} \\\\ \cos(2\varphi) &=& \dfrac{c}{x} \\\\ \mathbf{c} &=&\mathbf{ x\cos(2\varphi)} \qquad (2) \\ \hline \end{array} \\ \begin{array}{|lrcll|} \hline (1)=(2): & c = \mathbf{ 9\cos(\varphi)} &=& \mathbf{ x\cos(2\varphi)} \\\\ & 9\cos(\varphi) &=& x\cos(2\varphi) \\\\ & \mathbf{x} &=& \mathbf{\dfrac{9\cos(\varphi) } {\cos(2\varphi)}} \\\\ & x &=& \dfrac{9\cos(\varphi) } {\cos^2(\varphi)-\sin^2(\varphi)} \\\\ & x\Big(\cos^2(\varphi)-\sin^2(\varphi)\Big) &=& 9\cos(\varphi) \quad | \quad : \cos^2(\varphi) \\\\ & x\Big(1-\tan^2(\varphi)\Big) &=& \dfrac{9}{\cos(\varphi)} \quad | \quad \dfrac{1}{\cos(\varphi)} = \sqrt{1+\tan^2(\varphi) } \\\\ & x\Big(1-\tan^2(\varphi)\Big) &=& 9\sqrt{1+\tan^2(\varphi) } \\\\ & \mathbf{x} &=& \mathbf{\dfrac{9\sqrt{1+\tan^2(\varphi) }} {1-\tan^2(\varphi)}} \qquad (3) \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{\text{In }\triangle ACD:} \\ \hline \sin(45^\circ+\varphi) &=& \dfrac{a}{8\sqrt{2}} \\\\ \dfrac{\sqrt{2}}{2}\Big(\sin(\varphi)+\cos(\varphi) \Big) &=& \dfrac{a}{8\sqrt{2}} \\\\ 8\Big(\sin(\varphi)+\cos(\varphi) \Big) &=& a \\\\ \mathbf{a} &=&\mathbf{8\Big(\sin(\varphi)+\cos(\varphi) \Big)} \qquad (4) \\ \hline \end{array} \begin{array}{|rcll|} \hline \mathbf{\text{In }\triangle ABC:} \\ \hline \sin(2\varphi) &=& \dfrac{a}{x} \quad | \quad \sin(2\varphi)=\dfrac{2\tan(\varphi)}{1+\tan^2(\varphi)} \\\\ \dfrac{2\tan(\varphi)}{1+\tan^2(\varphi)} &=& \dfrac{a}{x} \\\\ \mathbf{a} &=& \mathbf{\dfrac{2x\tan(\varphi)}{1+\tan^2(\varphi)}} \qquad (5) \\ \hline \end{array} \\ \begin{array}{|lrcll|} \hline (4)=(5): & a = \mathbf{8\Big(\sin(\varphi)+\cos(\varphi) \Big)} &=& \mathbf{\dfrac{2x\tan(\varphi)}{1+\tan^2(\varphi)}} \\\\ & 8\Big(\sin(\varphi)+\cos(\varphi) \Big) &=& \dfrac{2x\tan(\varphi)}{1+\tan^2(\varphi)} \\\\ & 4\Big(\sin(\varphi)+\cos(\varphi) \Big) &=& \dfrac{x\tan(\varphi)}{1+\tan^2(\varphi)} \quad | \quad \cos(\varphi) = \dfrac{1}{ \sqrt{1+\tan^2(\varphi)} } \\\\ & 4\left(\dfrac{1}{ \sqrt{1+\tan^2(\varphi)} } +\sin(\varphi) \right) &=& \dfrac{x\tan(\varphi)}{1+\tan^2(\varphi)} \quad | \quad \sin(\varphi) = -\dfrac{\tan(\varphi)}{ \sqrt{1+\tan^2(\varphi)} } \\\\ & 4\left(\dfrac{1}{ \sqrt{1+\tan^2(\varphi)} } -\dfrac{\tan(\varphi)}{ \sqrt{1+\tan^2(\varphi)} } \right) &=& \dfrac{x\tan(\varphi)}{1+\tan^2(\varphi)} \\\\ & \dfrac{ 4\Big( 1-\tan(\varphi) \Big) } { \sqrt{1+\tan^2(\varphi)} } &=& \dfrac{x\tan(\varphi)}{1+\tan^2(\varphi)} \\\\ & 4\Big( 1-\tan(\varphi) \Big) &=& \dfrac{x\tan(\varphi)\sqrt{1+\tan^2(\varphi)}}{1+\tan^2(\varphi)} \\\\ & 4\Big( 1-\tan(\varphi) \Big) &=& \dfrac{x\tan(\varphi)}{\sqrt{1+\tan^2(\varphi)}} \\\\ & \mathbf{x} &=& \mathbf{ \dfrac{4\sqrt{1+\tan^2(\varphi)}\Big( 1-\tan(\varphi) \Big) } {\tan(\varphi)} } \qquad (6)\\ \hline \end{array}\)

\(\begin{array}{|lrcll|} \hline (3)=(6): & x = \mathbf{\dfrac{9\sqrt{1+\tan^2(\varphi) }} { 1-\tan^2(\varphi)} } &=& \mathbf{ \dfrac{4\sqrt{1+\tan^2(\varphi)}\Big( 1-\tan(\varphi) \Big) } {\tan(\varphi)} } \\\\ & \dfrac{9} { 1-\tan^2(\varphi)} &=& \dfrac{4\Big( 1-\tan(\varphi) \Big) } {\tan(\varphi)} \\\\ & \dfrac{9}{4}*\tan(\varphi) &=& \Big( 1-\tan^2(\varphi)\Big) \Big( 1-\tan(\varphi) \Big) \\\\ & \dfrac{9}{4}*\tan(\varphi) &=& 1-\tan(\varphi) - \tan^2(\varphi)+\tan^3(\varphi) \\\\ & \ldots \\ & \mathbf{\tan^3(\varphi) -\tan^2(\varphi)+\dfrac{5}{4}*\tan(\varphi)+1} &=& \mathbf{0} \\ & \Rightarrow \varphi &=& \arctan(\dfrac{1}{2}) \\ &\mathbf{\varphi} &=& \mathbf{26.5650511771^\circ} \\ \hline \end{array} \)

\(\begin{array}{|rcll|} \hline \mathbf{x} &=& \mathbf{\dfrac{9\cos(\varphi) } {\cos(2\varphi)}} \\\\ x &=& \dfrac{9\cos(26.5650511771^\circ) } {\cos(2*26.5650511771^\circ)} \\\\ x &=& \dfrac{8.04984471900} {0.6} \\\\ \mathbf{x} &=& \mathbf{13.4164078650} \\ \hline \end{array}\)

Solve for x:
\(\ln \left( x \dfrac { 1 } { \ln \left( x \dfrac{ 1 } { \ln \left( x \dfrac { 1 } { \ln \left( x \cdot \cdots \right) } \right) } \right) } \right) = \mathrm{e}\)

\(\begin{array}{|rcll|} \hline e &=& \ln\left(x*\dfrac{1}{e}\right) \\\\ e^e &=& \dfrac{x}{e} \\\\ e^ee &=& x \\ x &=& e^ee \\ \mathbf{x} &=& \mathbf{e^{e+1}} \\ \mathbf{x} &=& \mathbf{41.1935556747} \\ \hline \end{array}\)

If

\(z\) is a complex number satisfying \(z + \dfrac{1}{z} =1\), calculate \(z^{10}+ \dfrac{1}{z^{10}}\). 

\(\begin{array}{|rcll|} \hline \left( z+\dfrac{1}{z} \right)^2 &=& z^2+\dfrac{1}{z^2} + \dfrac{2z}{z} \\\\ 1^2 &=& z^2+\dfrac{1}{z^2} + 2 \\\\ z^2+\dfrac{1}{z^2} &=& 1-2 \\\\ \mathbf{z^2+\dfrac{1}{z^2}} &=& \mathbf{-1} \\ \hline \end{array} \begin{array}{|rcll|} \hline \left( z^2+\dfrac{1}{z^2} \right)\left( z+\dfrac{1}{z} \right) &=& z^3+\dfrac{1}{z^3} + z+\dfrac{1}{z} \\\\ (-1)*1 &=& z^3+\dfrac{1}{z^3} + 1 \\\\ z^3+\dfrac{1}{z^3} &=&-1-1 \\\\ \mathbf{z^3+\dfrac{1}{z^3}} &=& \mathbf{-2} \\ \hline \end{array}\\ \begin{array}{|rcll|} \hline \left( z^2+\dfrac{1}{z^2} \right)\left( z^3+\dfrac{1}{z^3} \right) &=& z^5+\dfrac{1}{z^5} + z+\dfrac{1}{z} \\\\ (-1)*(-2) &=& z^5+\dfrac{1}{z^5} + 1 \\\\ z^5+\dfrac{1}{z^5} &=&2-1 \\\\ \mathbf{z^5+\dfrac{1}{z^5}} &=& \mathbf{1} \\ \hline \end{array} \begin{array}{|rcll|} \hline \left( z^5+\dfrac{1}{z^5} \right)^2 &=& z^{10}+\dfrac{1}{z^{10}} +\dfrac{2z^5}{z^5} \\\\ 1^2 &=& z^{10}+\dfrac{1}{z^{10}} + 2 \\\\ z^{10}+\dfrac{1}{z^{10}} &=&1-2 \\\\ \mathbf{z^{10}+\dfrac{1}{z^{10}}} &=& \mathbf{-1} \\ \hline \end{array}\)

edited: Thank you Alan, thank you MaxWong

Thank you Guest !

In square ABCD shown, X is the midpoint of BC and Y is the midpoint of AX.
If CZ:ZD=3:1 and the side length of the square is 5 units, find YZ.

\(\begin{array}{|rcll|} \hline \mathbf{ZD} &=& \dfrac{1}{1+3}*5 \\\\ &=& \dfrac{5}{4} \\\\ &=& \mathbf{1.25} \\\\ \mathbf{CZ} &=& \dfrac{3}{1+3}*5 \\\\ &=& \dfrac{15}{4} \\\\ &=& \mathbf{3.75} \\\\ \mathbf{z} &=& 5-ZD-2.5\\ &=& 5-1.25-2.5\\ &=& \mathbf{1.25} \\ \hline \end{array} \begin{array}{|rcll|} \hline \text{Intercept theorem:}\\ \hline \mathbf{\dfrac{2.5}{5-y}} &=& \mathbf{\dfrac{5}{2.5}} \\\\ \dfrac{5-y}{2.5} &=& \dfrac{2.5}{5} \\\\ 5-y &=& \dfrac{2.5^2}{5} \\\\ y &=& 5-\dfrac{2.5^2}{5} \\\\ y &=& \dfrac{25-2.5^2}{5} \\\\ \mathbf{ y } &=& \mathbf{3.75} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline x^2 &=& y^2+z^2 \\ x^2 &=& 3.75^2+1.25^2 \\ x^2 &=& 15.625 \\ \mathbf{x} &=& \mathbf{3.95284707521} \\ \hline \end{array}\)

\(YZ\) is \(\approx \mathbf{3.95}\)

calc- integration

\(\int \dfrac{1}{1-\sin(x)} \ dx\)

\(\begin{array}{|rclcrcl|} \hline && \mathbf{\int \dfrac{1}{1-\sin(x)} dx } \\\\ &=& \int \dfrac{1}{\Big(1-\sin(x)\Big)}*\dfrac{\Big(1+\sin(x)\Big)}{\Big(1+\sin(x)\Big)} dx \\\\ &=& \int \dfrac{1+\sin(x)}{1-\sin^2(x)} dx \quad | \quad 1-\sin^2(x)=\cos^2(x) \\\\ &=& \int \dfrac{1+\sin(x)}{ \cos^2(x)} dx \\\\ &=& \int \left( \dfrac{1}{ \cos^2(x)}+\dfrac{\sin(x)}{ \cos^2(x)}\right) dx \\\\ &=& \mathbf{\int \dfrac{1}{ \cos^2(x)} dx +\int \dfrac{\sin(x)}{ \cos^2(x)} dx } \\ \hline \end{array} \)

\(\begin{array}{|rclcrcl|} \hline && \mathbf{ \int \dfrac{1}{ \cos^2(x)} dx } \\\\ && \text{substitute:} & u&=& \tan(x) \\\\ && & u&=& \dfrac{\sin(x)}{\cos(x)} \\\\ && & du&=& \dfrac{\cos(x)\cos(x)-\sin(x)(-\sin(x)}{\cos^2(x)}\ dx \\\\ && & du&=& \dfrac{\cos^2(x)+\sin^2(x)}{\cos^2(x)} \ dx\\\\ && & du&=& \dfrac{1}{\cos^2(x)} \ dx \\\\ && & dx&=& \cos^2(x) \ du \\\\ &=& \int \dfrac{1}{ \cos^2(x)} \cos^2(x) \ du \\\\ &=& \int \ du \\\\ &=& u \\\\ \mathbf{ \int \dfrac{1}{ \cos^2(x)} dx }&=& \mathbf{ \tan(x) }+c \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline && \mathbf{\int \dfrac{\sin(x)}{ \cos^2(x)} dx } \\\\ &=& -\int \dfrac{-\sin(x)}{ \cos^2(x)} dx \\\\ && \text{substitute:} & u&=& \cos(x) \\\\ && & du&=& -\sin(x) \ dx \\\\ &=& -\int \dfrac{1}{u^2} du \\\\ &=& -\int u^{-2} du \\\\ &=& - \dfrac{u^{-2+1}}{-2+1} \\\\ &=& - \dfrac{u^{-1}}{-1} \\\\ &=& u^{-1} \\\\ &=& \dfrac{1}{u} \\\\ \mathbf{\int \dfrac{\sin(x)}{ \cos^2(x)} dx }&=& \mathbf{ \dfrac{1}{\cos(x)} +c} \\ \hline \end{array} \)

\(\begin{array}{|rclcrcl|} \hline && \mathbf{\int \dfrac{1}{1-\sin(x)} dx } \\\\ &=& \mathbf{\int \dfrac{1}{ \cos^2(x)} dx +\int \dfrac{\sin(x)}{ \cos^2(x)} dx } \\\\ &=& \mathbf{\tan(x) + \dfrac{1}{\cos(x)} +c} \\ \hline \end{array}\)

How can i calculate cosh with complex number?

If

\(abc = 13 \)

and
\(\left(a+\dfrac{1}{b}\right)\left(b+\dfrac{1}{c}\right)\left(c+\dfrac{1}{a}\right)=\left(1+\dfrac{1}{a}\right)\left(1+\dfrac{1}{b}\right)\left(1+\dfrac{1}{c}\right)\),
find \(a + b + c\).

\(\small{ \begin{array}{|rcll|} \hline \mathbf{\left(a+\dfrac{1}{b}\right)\left(b+\dfrac{1}{c}\right)\left(c+\dfrac{1}{a}\right) } &=& \mathbf{\left(1+\dfrac{1}{a}\right)\left(1+\dfrac{1}{b}\right)\left(1+\dfrac{1}{c}\right)} \\\\ \left(\dfrac{ab+1}{b}\right)\left(\dfrac{bc+1}{c}\right)\left(\dfrac{ca+1}{a}\right) &=& \left(\dfrac{1+a}{a}\right)\left(\dfrac{1+b}{b}\right)\left(\dfrac{1+c}{c}\right) \\\\ \dfrac{(ab+1)(bc+1)(ca+1)}{abc} &=& \dfrac{(1+a)(1+b)(1+c)}{abc} \\\\ \dfrac{(ab+1)(bc+1)(ca+1)}{abc}-\dfrac{(1+a)(1+b)(1+c)}{abc} &=& 0 \\\\ \dfrac{(ab+1)(bc+1)(ca+1)-(1+a)(1+b)(1+c)}{abc} &=& 0 \\\\ (ab+1)(bc+1)(ca+1)-(1+a)(1+b)(1+c) &=& 0 \\\\ (ab^2c+ab+bc+1)(ca+1)-(ab+a+b+1)(c+1) &=& 0 \\ a^2b^2c^2+a^2bc+abc^2+ca+ab^2c+ab+bc+1-(abc+ab+ac+a+bc+b+c+1) &=& 0 \\ a^2b^2c^2+a^2bc+abc^2+ca+ab^2c+ab+bc+1-abc-ab-ac-a-bc-b-c-1 &=& 0 \\ a^2b^2c^2+a^2bc+abc^2+ab^2c-abc-a-b-c &=& 0 \\ abc(abc+a+b+c)-(abc+a+b+c) &=& 0 \\ (abc-1)(abc+a+b+c) &=& 0 \quad | \quad abc= 13 \\ (13-1)(13+a+b+c) &=& 0 \\ 12(13+a+b+c) &=& 0 \\ 13+a+b+c &=& 0 \\ \mathbf{a+b+c} &=& \mathbf{-13} \\ \hline \end{array} } \)