heureka

If xy = 7 and x + y = 5, then find \(x^3 + y^3\).

1.

\(\begin{array}{|rcll|} \hline (x + y)^2 &=& x^2+2xy+y^2 \\ 5^2 &=& x^2+2*7+y^2 \\ x^2+y^2 &=& 25-14 \\ \mathbf{x^2+y^2} &=& \mathbf{11} \\ \hline \end{array}\)

2.

\(\begin{array}{|rcll|} \hline (x^2+y^2)(x+y) &=& x^3+x^2y+y^2x+y^3 \\ 11*5 &=& x^3+y^3+xy(x+y) \\ 55 &=& x^3+y^3+7*5 \\ x^3+y^3 &=& 55 -35 \\ \mathbf{x^3+y^3} &=& \mathbf{20} \\ \hline \end{array}\)

Solve for x:
\(\large \dfrac{\color{red}{ \sqrt{2x-1} }+\color{green}{\sqrt{2x+1}} }{\color{green}{ \sqrt{2x+1}}-\color{red}{\sqrt{2x-1}} }=\color{blue}{\dfrac{5}{3}} \quad, \quad \color{magenta}{x} = \ ?\)

\(\begin{array}{|rcll|} \hline \dfrac{\color{red}{ \sqrt{2x-1} }+\color{green}{\sqrt{2x+1}} }{\color{green}{ \sqrt{2x+1}}-\color{red}{\sqrt{2x-1}} } &=& \color{blue}{\dfrac{5}{3}} \\\\ \dfrac{ \color{red}{ \Big(\sqrt{2x-1} }+\color{green}{\sqrt{2x+1}} \Big)} { \color{green}{ \Big( \sqrt{2x+1}}-\color{red}{\sqrt{2x-1}} \Big) } * \dfrac{ \Big( \sqrt{2x-1}+ \sqrt{2x+1} \Big)} { \Big( \sqrt{2x+1}+ \sqrt{2x-1} \Big) } &=& \color{blue}{\dfrac{5}{3}} \\\\ \dfrac{ \Big( \sqrt{2x-1}+ \sqrt{2x+1} \Big)^2} { 2x+1-(2x-1) } &=& \color{blue}{\dfrac{5}{3}} \\\\ \dfrac{ 2x-1 +2\sqrt{(2x-1)(2x+1)}+2x+1 } { 2x+1-(2x-1) } &=& \color{blue}{\dfrac{5}{3}} \\\\ \dfrac{ 4x +2\sqrt{(2x-1)(2x+1)} } { 2x+1-2x+1 } &=& \color{blue}{\dfrac{5}{3}} \\\\ \dfrac{ 4x +2\sqrt{(2x-1)(2x+1)} } { 2 } &=& \color{blue}{\dfrac{5}{3}} \\\\ \dfrac{ 4x +2\sqrt{4x^2-1} } { 2 } &=& \color{blue}{\dfrac{5}{3}} \\\\ 2x +\sqrt{4x^2-1} &=& \color{blue}{\dfrac{5}{3}} \\\\ \sqrt{4x^2-1} &=& \color{blue}{\dfrac{5}{3}} - 2x \quad | \quad \text{square both sides} \\\\ 4x^2-1 &=& \left( \color{blue}{\dfrac{5}{3}} - 2x\right)^2 \\\\ 4x^2-1 &=& \dfrac{25}{9}-\dfrac{20x}{3} + 4x^2 \\\\ -1 &=& \dfrac{25}{9}-\dfrac{20x}{3} \\\\ \dfrac{20x}{3} &=& \dfrac{25}{9} + 1 \\\\ \dfrac{20x}{3} &=& \dfrac{34}{9} \\\\ x &=& \dfrac{34}{9}* \dfrac{3}{20} \\\\ x &=& \dfrac{17}{3*10} \\\\ \mathbf{x} &=& \mathbf{\dfrac{17}{30}} \\ \hline \end{array}\)

Circle A, with a radius of 9, has a horizontal chord BC with a length of 10.
From point C, a vertical line extends to point D.
From point D, a horizontal line extends to point E on the circle's circumference.
Line segment DE has a length of 3.
From point E, another vertical line extends to point F on the circle's circumference.
Points B and D connect to form a line segment, and so do points D and F.
What is the angle (in degrees) of \(\angle BDF\)?

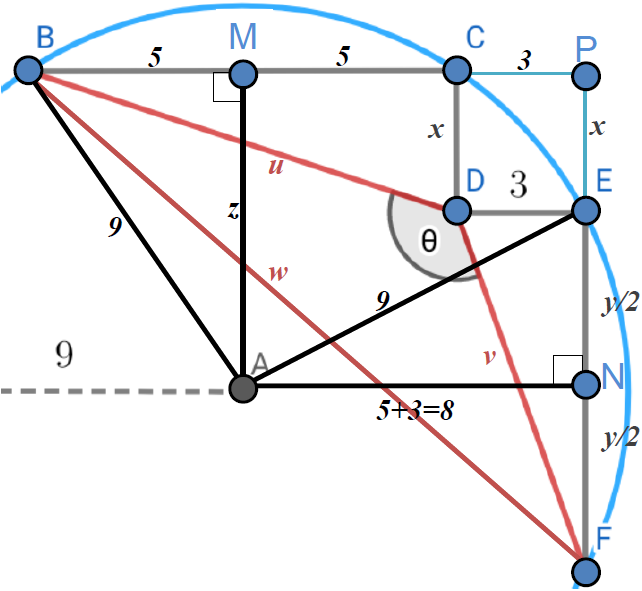
\(\begin{array}{|rcll|} \hline \mathbf{\text{In }\triangle AEN:} \\ \hline \dfrac{y^2}{4} + 8^2 &=& 9^2 \\\\ \dfrac{y^2}{4} &=& 9^2- + 8^2 \\\\ \dfrac{y^2}{4} &=& 17 \\\\ \mathbf{y^2} &=& \mathbf{68} \\ \mathbf{y} &=& \mathbf{2\sqrt{17}} \\ \hline \end{array} \begin{array}{|rcll|} \hline \mathbf{\text{In }\triangle DEF:} \\ \hline v^2 &=& 3^2 + y^2 \\ v^2 &=& 9+68 \\ \mathbf{v^2} &=& \mathbf{77} \\ \mathbf{v} &=& \mathbf{\sqrt{77}} \\ \hline \end{array} \begin{array}{|rcll|} \hline \mathbf{\text{In }\triangle BMA:} \\ \hline 5^2+z^2 &=& 9^2 \\ z^2 &=& 81-25 \\ z^2 &=& 56 \\ \mathbf{z} &=& \mathbf{2\sqrt{14}} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline x + \dfrac{y}{2} &=& z \\\\ x &=& z- \dfrac{y}{2} \\\\ x &=& 2\sqrt{14}- \dfrac{2\sqrt{17}}{2} \\\\ \mathbf{x} &=& \mathbf{2\sqrt{14}- \sqrt{17}} \\ \hline \end{array} \begin{array}{|rcll|} \hline \mathbf{\text{In }\triangle BCD:} \\ \hline u^2 &=& 10^2+x^2 \\ u^2 &=& 100+ \left( 2\sqrt{14}- \sqrt{17} \right)^2 \\ u^2 &=& 100+ 4*14-4\sqrt{14*17} + 17 \\ \mathbf{u^2} &=& \mathbf{173-4\sqrt{238}} \\ \mathbf{u} &=& \mathbf{\sqrt{173-4\sqrt{238}}} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{\text{In }\triangle BPF:} \\ \hline w^2 &=& 13^2 +(x+y)^2 \\ w^2 &=& 13^2 +\left( 2\sqrt{14}- \sqrt{17}+2\sqrt{17} \right)^2 \\ w^2 &=& 13^2 +\left( 2\sqrt{14}+\sqrt{17} \right)^2 \\ w^2 &=& 13^2 +4*14+4\sqrt{14*17} + 17 \\ \mathbf{w^2} &=& \mathbf{242+4\sqrt{238}} \\ \hline \end{array}\)

cos-rule:

\(\begin{array}{|rcll|} \hline \mathbf{\text{In }\triangle BDF:} \\ \hline \mathbf{w^2} &=& \mathbf{u^2+v^2-2uv\cos(\theta)} \\\\ \cos(\theta) &=& \dfrac{u^2+v^2-w^2}{2uv} \\\\ \cos(\theta) &=& \dfrac{173-4\sqrt{238}+77-(242+4\sqrt{238})}{2\sqrt{173-4\sqrt{238}}\sqrt{77}} \\\\ \cos(\theta) &=& \dfrac{8-8\sqrt{238}} {2\sqrt{13321-308\sqrt{238}}} \\\\ \cos(\theta) &=& \dfrac{4(1-\sqrt{238})} {\sqrt{13321-308\sqrt{238}}} \\\\ \cos(\theta) &=& \dfrac{-57.7089944822} {92.5710938948} \\\\ \cos(\theta) &=& -0.62340188556 \\ \theta &=& \arccos(-0.62340188556) \\ \mathbf{\theta} &=& \mathbf{128.564985997^\circ} \\ \hline \end{array}\)

The angle (in degrees) of \(\angle BDF\) is \(\mathbf{128.564985997^\circ}\)

I need help with this system:
\(\begin{eqnarray} x(y+z)&=&39\\ y(x+z)&=&60\\ z(x+y)&=&63 \\ x^2+y^2+z^2&=& \ ? \end{eqnarray}\)

\(\begin{array}{|lrcll|} \hline & x(y+z)&=&39 \\ & xy+xz &=& 39 \\ & \mathbf{xz} &=& \mathbf{39-xy} \qquad (1) \\\\ & y(x+z)&=&60 \\ & yx+yz &=&60 \\ & \mathbf{yz} &=& \mathbf{60-xy} \qquad (2) \\ \hline (1)+(2): & xz+yz &=& 39-xy+60-xy \\ & z(x+y) &=& 99-2xy \quad | \quad \mathbf{z(x+y)=63} \\ & 63 &=& 99-2xy \\ & 2xy &=& 99-63 \\ & 2xy &=& 36 \\ & \mathbf{xy} &=& \mathbf{18} \quad \text{or} \quad \mathbf{y=\dfrac{18}{x}} \qquad (3) \\ \hline \end{array} \)

\(\begin{array}{|rcll|} \hline x(y+z)&=& 39 \quad | \quad \mathbf{y=\dfrac{18}{x}} \\\\ x\left(\dfrac{18}{x}+z\right) &=& 39 \\\\ 18 +xz &=& 39 \\\\ xz &=& 39-18 \\\\ \mathbf{xz} &=& \mathbf{21} \quad \text{or} \quad \mathbf{x=\dfrac{21}{z}} \qquad (4) \\ \hline \end{array} \)

\(\begin{array}{|rcll|} \hline z(x+y)&=& 63 \quad | \quad \mathbf{x=\dfrac{21}{z}} \\\\ z\left(\dfrac{21}{z}+y \right)&=& 63 \\\\ 21+zy &=& 63 \\\\ zy &=& 63-21 \\\\ \mathbf{zy} &=& \mathbf{42} \qquad (5) \\ \hline \end{array}\)

\(\begin{array}{|lrcll|} \hline \dfrac{(3)}{(5)}: & \dfrac{xy}{zy} &=& \dfrac{18}{42} \\\\ & \dfrac{x}{z} &=& \dfrac{3}{7} \quad | \quad \mathbf{x=\dfrac{21}{z}}\quad \text{or} \quad \mathbf{z=\dfrac{21}{x}} \\\\ & \dfrac{x}{\dfrac{21}{x}} &=& \dfrac{3}{7} \\\\ & \dfrac{x^2}{21} &=& \dfrac{3}{7} \\\\ & x^2 &=& \dfrac{3*21}{7} \\\\ & x^2 &=& 3*3 \\\\ & \mathbf{x} &=& \pm \mathbf{3} \\ \hline & \mathbf{y} &=& \mathbf{\dfrac{18}{x}} \\\\ & y &=& \dfrac{18}{\pm 3} \\\\ & \mathbf{y} &=& \mathbf{\pm 6 } \\ \hline & \mathbf{z} &=& \mathbf{\dfrac{21}{x} } \\\\ & z &=& \dfrac{21}{\pm 3} \\\\ & \mathbf{z} &=& \mathbf{\pm 7} \\ \hline & x^2+y^2+z^2 &=& (\pm 3)^2+(\pm 6)^2+(\pm 7)^2 \\\\ & &=& 9+36+49 \\\\ &\mathbf{ x^2+y^2+z^2} &=& \mathbf{94} \\ \hline \end{array}\)

(b) Compute the sum

\(\Big(a +(2n+1)d\Big)^2- \Big(a + (2n)d\Big)^2 +\Big(a + (2n-1)d\Big)^2 - \Big(a+(2n-2)d\Big)^2 + \cdots + (a+d)^2 - a^2.\).

\(\small{ \begin{array}{|rcll|} \hline && \mathbf{\Big(a +(2n+1)d\Big)^2- \Big(a + (2n)d\Big)^2 +\Big(a + (2n-1)d\Big)^2 - \Big(a+(2n-2)d\Big)^2 + \cdots + (a+d)^2 - a^2} \\\\ &=& \Big(a +(2n+1)d\Big)^2 +\Big(a + (2n-1)d\Big)^2+\Big(a + (2n-3)d\Big)^2 + \cdots + \Big(a+(2n-(2n-1))d\Big)^2 \\ && -\Big(a + (2n-0)d\Big)^2- \Big(a+(2n-2)d\Big)^2- \Big(a+(2n-4)d\Big)^2 - \cdots -\Big(a+(2n-(2n))d\Big)^2 \\\\ &=& \mathbf{\sum \limits_{k=1}^{n+1}\Big(~ a+(2k-1)d~\Big)^2 -\sum \limits_{k=1}^{n+1}\Big(~ a+2(k-1)d~\Big)^2} \\ \hline \end{array} }\)

\(\begin{array}{|rcll|} \hline && \mathbf{\sum \limits_{k=1}^{n+1}\Big(~ a+(2k-1)d~\Big)^2 -\sum \limits_{k=1}^{n+1}\Big(~ a+2(k-1)d~\Big)^2} \\\\ &=& \sum \limits_{k=1}^{n+1}\Big(~ a+(2k-1)d~\Big)^2 - \Big(~a+2(k-1)d~\Big)^2 \\\\ &=& \sum \limits_{k=1}^{n+1} a^2+2ad(2k-1)+d^2(2k-1)^2-\Big(~ a^2+4ad(k-1)+4d^2(k-1)^2 ~\Big) \\\\ &=& \sum \limits_{k=1}^{n+1} {\color{red}{a^2}}+2ad(2k-1)+d^2(2k-1)^2 {\color{red}{-a^2}}-4ad(k-1)-4d^2(k-1)^2 \\\\ &=& \sum \limits_{k=1}^{n+1} 2ad(2k-1)+d^2(2k-1)^2 -4ad(k-1)-4d^2(k-1)^2 \\\\ &=& \sum \limits_{k=1}^{n+1} {\color{red}{4adk}}-2ad+d^2(2k-1)^2 {\color{red}{-4adk}}+4ad-4d^2(k-1)^2 \\\\ &=& \sum \limits_{k=1}^{n+1} -2ad+d^2(2k-1)^2 +4ad-4d^2(k-1)^2 \\\\ &=& \sum \limits_{k=1}^{n+1} 2ad+d^2(2k-1)^2 -4d^2(k-1)^2 \\\\ &=& \sum \limits_{k=1}^{n+1}2ad +d^2~\sum \limits_{k=1}^{n+1} (2k-1)^2 -4(k-1)^2 \quad | \quad \sum \limits_{k=1}^{n+1}2ad = 2ad(n+1) \\\\ &=& 2ad(n+1) +d^2\sum \limits_{k=1}^{n+1} (2k-1)^2 -4(k-1)^2 \\\\ &=& 2ad(n+1) +d^2\sum \limits_{k=1}^{n+1} 4k^2-4k+1-4(k^2-2k+1) \\\\ &=& 2ad(n+1) +d^2\sum \limits_{k=1}^{n+1} {\color{red}{4k^2}}-4k+1{\color{red}{-4k^2}}+8k-4 \\\\ &=& 2ad(n+1) +d^2\sum \limits_{k=1}^{n+1} 4k-3 \\\\ &=& 2ad(n+1) +d^2\Big(~4\sum \limits_{k=1}^{n+1}k-\sum \limits_{k=1}^{n+1}3~\Big)\quad | \quad \sum \limits_{k=1}^{n+1}3 = 3(n+1) \\\\ &=& 2ad(n+1) +d^2\Big(~4\sum \limits_{k=1}^{n+1}k-3(n+1)~\Big) \\\\ &=& 2ad(n+1) +d^2\Big(~4\sum \limits_{k=1}^{n+1}k-3(n+1)~\Big) \quad | \quad \sum \limits_{k=1}^{n+1}k = \dfrac{1+(n+1)}{2}(n+1) \\\\ &=& 2ad(n+1) +d^2\Big(~4\dfrac{(n+2))}{2}(n+1)-3(n+1)~\Big) \\\\ &=& 2ad(n+1) +d^2\Big(~2(n+2)(n+1)-3(n+1)~\Big) \\\\ &=& 2ad(n+1) +d^2(n+1)\Big(~2(n+2)-3~\Big) \\\\ &=& 2ad(n+1) +d^2(n+1)(2n+4-3) \\\\ &=& 2ad(n+1) +d^2(n+1)(2n+1) \\ &=& \mathbf{d(n+1)\Big(2a+d(2n+1)\Big)} \\ \hline \end{array}\)

\(\mathbf{\Big(a +(2n+1)d\Big)^2- \Big(a + (2n)d\Big)^2 +\Big(a + (2n-1)d\Big)^2 - \Big(a+(2n-2)d\Big)^2 + \cdots + (a+d)^2 - a^2} \\ = \mathbf{d(n+1)\Big(2a+d(2n+1)\Big)}\)

(a) Compute the sum:
\(101^2-97^2+93^2-89^2+\ldots+5^2-1^2\)

\(\begin{array}{|rcll|} \hline && \mathbf{ 101^2-97^2+93^2-89^2+\ldots+5^2-1^2} \\\\ &=& 101^2 + 93^2 + 85^2 +\ldots+ 13^2+5^2 \\ && -97^2 -89^2 -81^2 -\ldots- 9^2-1^2 \\\\ &=& \mathbf{\sum \limits_{k=1}^{13}\Big(~ 8k-3~\Big)^2 -\sum \limits_{k=1}^{13}\Big(~ 8k-7~\Big)^2} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline && \mathbf{\sum \limits_{k=1}^{13}\Big(~ 8k-3~\Big)^2 -\sum \limits_{k=1}^{13}\Big(~ 8k-7~\Big)^2} \\\\ &=& \sum \limits_{k=1}^{13}\Big(~ 8k-3~\Big)^2 - \Big(~ 8k-7~\Big)^2 \\\\ &=& \sum \limits_{k=1}^{13}64k^2-48k+9-(64k^2-112k+49) \\\\ &=& \sum \limits_{k=1}^{13} {\color{red}64k^2}-48k+9{\color{red}-64k^2}+112k-49 \\\\ &=& \sum \limits_{k=1}^{13} -48k+9+112k-49 \\\\ &=& \sum \limits_{k=1}^{13} 64k-40 \\\\ &=& 64\sum \limits_{k=1}^{13}k -\sum \limits_{k=1}^{13}40 \quad | \quad \sum \limits_{k=1}^{13}40 = 40*13 \\\\ &=& 64\sum \limits_{k=1}^{13}k - 40*13 \quad | \quad \sum \limits_{k=1}^{13}k = \dfrac{(1+13)}{2}*13 \\\\ &=& 64\dfrac{(1+13)}{2}*13 - 40*13 \\\\ &=& 32*14*13 - 40*13 \\\\ &=& 5824 - 520 \\\\ &=& \mathbf{5304} \\ \hline \end{array}\)

\(\mathbf{ 101^2-97^2+93^2-89^2+\ldots+5^2-1^2} = \mathbf{5304}\)

ABCD is a square with E, F, and G being the midpoints of CD, BC, and EF respectively. Let \(\angle\)DGE=x.

Find \(\tan(x)\).

\(\begin{array}{|rcll|} \hline \tan(y) &=& \dfrac{1}{4}\above 1pt \dfrac{3}{4} \\\\ \tan(y) &=& \dfrac{1}{4} * \dfrac{4}{3} \\\\ \tan(y) &=& \dfrac{1}{3} \\ \mathbf{y} &=& \mathbf{\arctan\left(\dfrac{1}{3}\right)} \\ \hline x+y &=& 45^\circ \\\\ x &=& 45^\circ - \arctan\left(\dfrac{1}{3}\right) \\ x &=& 45^\circ - 18.4349488229^\circ \\ \mathbf{x} &=& \mathbf{26.5650511771^\circ} \\ \hline \end{array}\)

Find the inradius of a triangle with 6, 25, and 29.

\(\text{Let $a=6$}\\ \text{Let $b=25$}\\ \text{Let $c=29$}\\ \text{Let the inradius of the triangle $= \rho$}\\ \text{Let $s=\dfrac{6+25+29}{2} = 30 $}\\ \text{Let the area of the triangle $A=\rho s $}\\ \text{Let the area of the triangle $A=\sqrt{s(s-a)(s-b)(s-c)} \quad (Heron) $}\)

\(\begin{array}{|rcll|} \hline A = \rho s &=& \sqrt{s(s-a)(s-b)(s-c)} \\\\ \rho s &=& \sqrt{s(s-a)(s-b)(s-c)} \\\\ \rho &=& \dfrac{ \sqrt{s(s-a)(s-b)(s-c)} } {s} \\\\ \rho &=& \sqrt{\dfrac{s(s-a)(s-b)(s-c)} {s^2} } \\\\ \mathbf{ \rho } &=& \mathbf{\sqrt{ \dfrac{ (s-a)(s-b)(s-c) } {s}}} \\\\ \rho &=& \sqrt{ \dfrac{ (30-6)(30-25)(30-29) } {30}} \\\\ \rho &=& \sqrt{ \dfrac{24*5*1 } {30}} \\\\ \rho &=& \sqrt{ \dfrac{120 } {30}} \\\\ \rho &=& \sqrt{4} \\\\ \mathbf{\rho} &=& \mathbf{2} \\ \hline \end{array}\)

The inradius of a triangle is \(\mathbf{2}\)

If A, B, C, D  are consecutive terms in an arithmetic progression,
what is the value of \(\dfrac{ D^2 - A^2 } { C^2 - B^2}\)
Assume \(B^2\) is not equal to \(C^2\).

AP:

\(\begin{array}{|rcll|} \hline A &=& a \\ B &=& a+d \\ C &=& a+2d \\ D &=& a+3d \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{\dfrac{ D^2 - A^2 } { C^2 - B^2}} &=& \dfrac{(D-A)(D+A)} { (C-B)(C+B)} \\\\ &=& \dfrac{(a+3d-a)(a+3d+a)} { \Big(a+2d-(a+d)\Big)(a+2d+a+d)} \\\\ &=& \dfrac{3d(2a+3d)} { (a+2d-a-d)(2a+3d)} \\\\ &=& \dfrac{3d(2a+3d)} { d(2a+3d)} \\\\ &=& \mathbf{3} \\ \hline \end{array}\)

Thank you, MaxWong